Respecto a la construcción o representación geométrica de los números complejos, no se sabe por qué, éstos, se representan con la parte imaginaria ortogonal a la parte real. En este sentido, el matemático inglés John Wallis (1616-1703) fue el primero en hacer una contribución importante a la representación de los mismos, ya que muestra una representación diferente a la que hoy día tenemos en la que la parte imaginaria no es ortogonal a la parte real. Esto marca la pauta para preguntarnos, ¿por qué elegimos la representación en la que la parte imaginaria es ortogonal a la parte real, y no elegimos la representación

geométrica dada por Wallis? Esta pregunta presupone, a su vez, que hay otra representación: la que hoy día tenemos de los números complejos. ¿Esta representación proviene de algún problema de naturaleza geométrica? El problema sobre la representación de los números complejos se puede dividir en tres actos: El primero, la imposibilidad de darle un sentido geométrico. Segundo, los intentos de darle un sentido geométrico. Y tercero, acerca de la compatiblidad de su cálculo con su correspondiente representación geométrica.

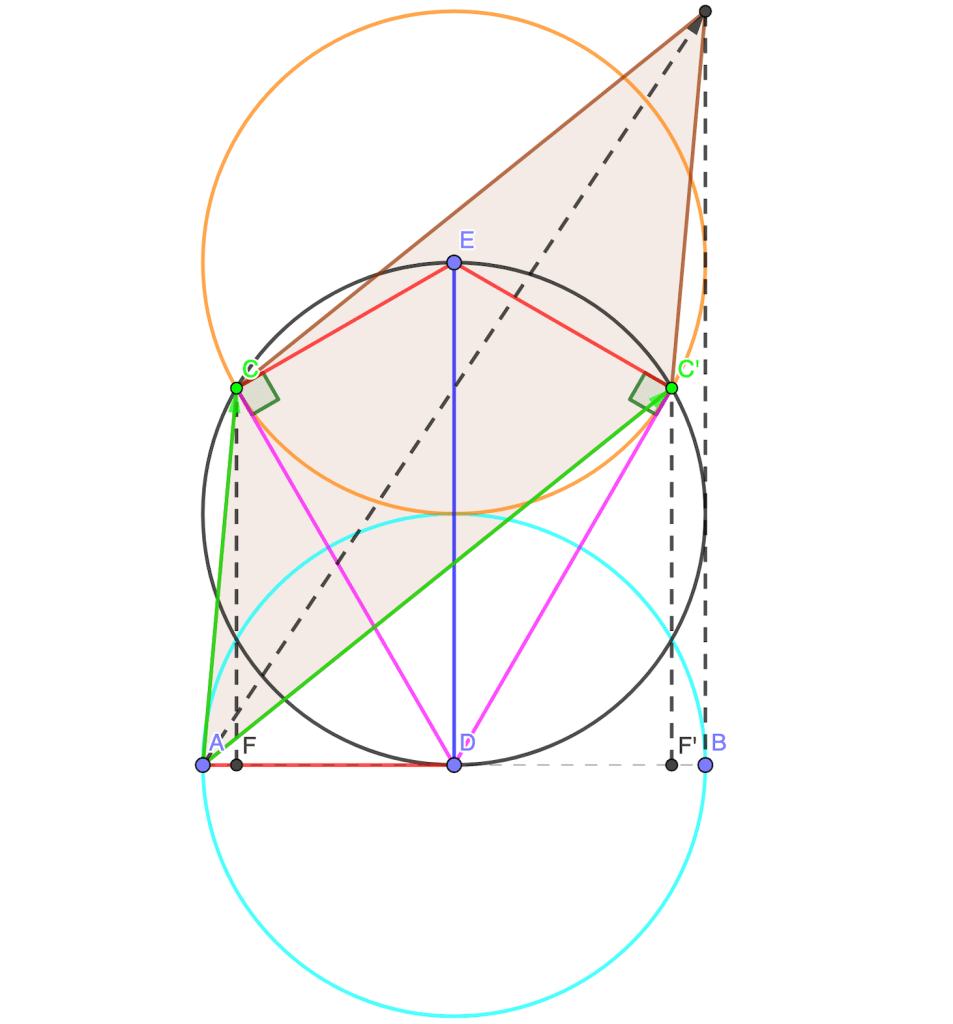
Dada la representación de las raíces complejas de la ecuación x²+b²=ax dada por John Wallis (1673) en la que la parte real e imaginaria no son ortogonales, como lo representamos hoy día, se puede observar que si bien, Wallis, no puede darle sentido a la suma de números complejos conjugados, asociados a las raíces de la ecuación cuadrática antes mencionada, cuya suma es a. Wallis muestra que las proyecciones de éstas –proyección de C y C’— al segmento AB (como se muestra en la figura), sí suman a (longitud del segmento AB). De esta forma, si consideramos el paralelogramo que forman estas raíces, AB coincide con la proyección de la diagonal sobre el segmento AB. Es decir, la representación geométrica de los números complejos, dada por Wallis, no es compatible con el cálculo de los mismos como expresiones algebraicas en las que se multiplican o suman como si multiplicase o sumase  números reales salvo que (√-1)²=-1. ¿Existe una representación de los números complejos cuyo cálculo sea compatible con su representación geométrica? En 1637 René Descartes lleva la solución del viejo problema de la

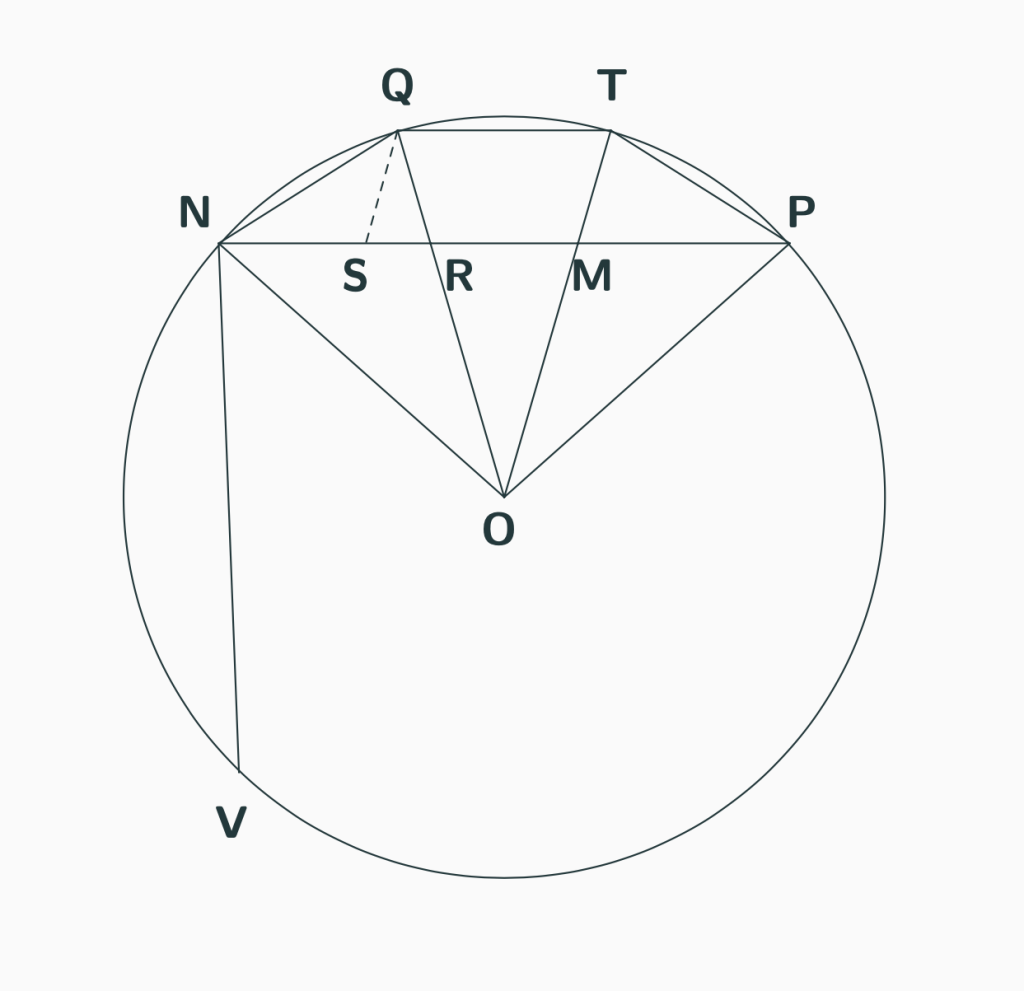
trisección de un ángulo (ver figura) a la solución de la ecuación cúbica x³+qr²=3r²x, donde q es la cuerda NP que determina el ángulo NOP a trisecar, r radio del círculo donde se inscribe el ángulo a trisecar y x (NQ o NV) la cuerda que subtiende la tercera parte del ángulo dado. Cuando q<2r, el problema tiene dos soluciones reales y, por ende, tres raíces reales. Ésta tercera raíz negativo de la suma de las otras dos, raíz positiva de la ecuación x³=Ax+B, aplicando las fórmulas Cardano para la misma, resulta que la condición para que esta ecuación tenga soluciones reales es, q>2r, haciendo A=3r², B=qr². ¿Dónde yace el absurdo? Equivalentemente, para que en la fórmula de Cardano que expresa la solución real de la ecuación cúbica aparezcan números complejos es, q<2r, así pues la raíz real se expresa, según las fórmulas de Cardano, como la suma de dos números complejos conjugados. ¿Existe un problema de naturaleza geométrica asociado a esta tercera raíz como el caso de las otras dos raíces asociadas a la trisección de ángulos conjugados?

El matemático suizo Leonhard Euler (1707-1783) publicó en 1749 una memoria cuyo titulo reza, «Sobre la controversia entre Leibniz&Bernoulli: Sobre la naturaleza del logaritmo de los números negativos». En ésta da respuesta a la pregunta: ¿cuál la naturaleza del logaritmo de un número negativo? ¿es real o complejo? o ¿cuál su naturaleza? Bernoulli creía que el logaritmo de los números negativos era real e igual al logaritmo del número positivo correspondiente: ln(-x)=ln(x). Si un punto se mueve continuamente sobre la hipérbola, su proyección sobre el eje «x» se moverá continuamente pasando del eje positivo al eje negativo a través del cero; y el punto sobre la rama positiva pasará a la rama negativa a través del infinito. Pasar de la rama positiva a la rama negativa a través del infinito viola el principio de continuidad. Las dos ramas no se pueden conectar a través del infinito. Supuesto que le permitió a Bernoulli deducir que ln(-x)=ln(x), ya que estos

valores de la rama negativa y positiva del logaritmo, respectivamente, son valores simétricos respecto al eje «y» a condición de que las dos ramas del logaritmo estén conectadas a través del infinito, es decir, se puede pasar de la rama positiva del logaritmo a la rama negativa (o simétrica) a través del infinito. Lo cual nuevamente viola el principio de continuidad, las dos ramas del logaritmo no se pueden conectar a través del infinito. Leibniz, sin embargo, creía que el logaritmo de los números negativos era complejo. Existe una forma de pasar de la rama positiva de la hipérbola a la rama negativa de la misma que no es a través del infinito. Si en lugar de recorrer sectores hiperbólicos, correspondientes al movimiento continuo de un punto sobre la hipérbola, recorremos un sector circular correspondiente a un ángulo de 180°. Pasar de una rama a otra de la hipérbola se hace a través del número complejo π√-1.