Equidescomposición

---

En la Antigüedad, la falta de una unidad en la geometría condujo a los geómetras a medir a través de comparar cantidades de la misma naturaleza (cantidades homogéneas). De esta forma, la equidescomposición: descomponer una figura en figuras menores y reordenarlas para formar otra figura de la misma área; y la equicomplementariedad: agregar figuras (de la misma área) a una figura dada para formar dos figuras de la misma área, fueron dos procedimientos que permitieron mostrar que, si a iguales les quitamos cosas iguales, lo que nos queda son cosas iguales. Si a iguales les agregamos cosas iguales, lo que resulta son cosas iguales. Así, pues, estos dos métodos permitieron a Euclides mostrar: 

Paralelogramos de la misma base y entre las mismas paralelas son iguales entre sí (paralelogramos que tienen la misma base y alturas iguales, tienen la misma área).

Lo anterior sin determinar una fórmula para el cálculo del área de un paralelogramo, ya que no había una unidad de medida.

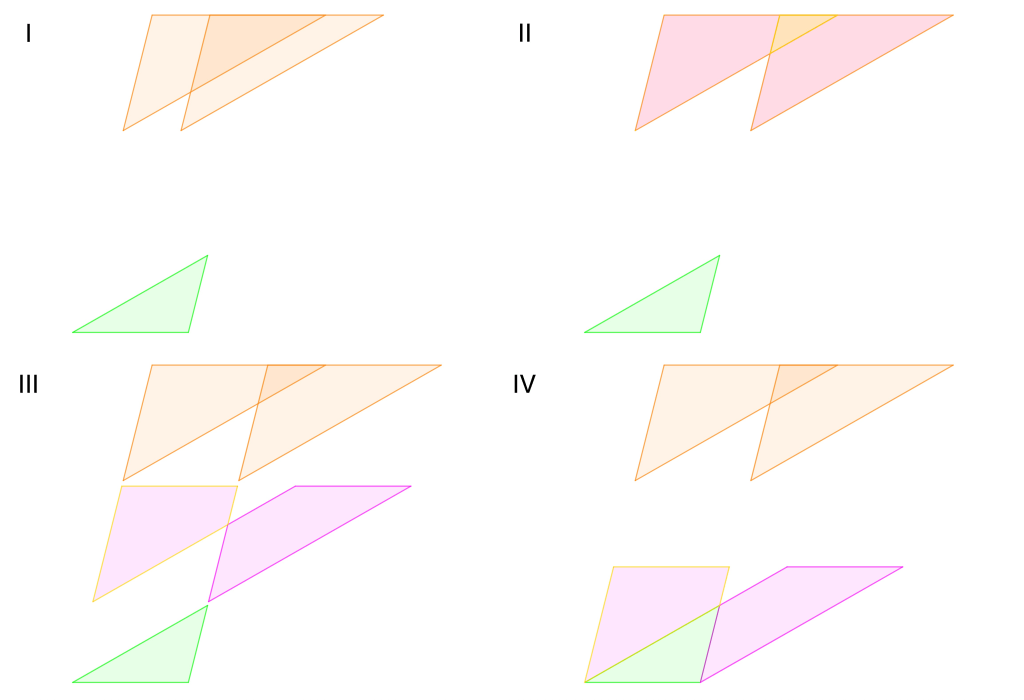
De izquierda a derecha y de arriba a abajo (ver la figura):

I: Traslación de un triángulo (pintado de naranja) no cambia su área.

II: Si a áreas iguales (triángulos naranjas) substraemos una misma área (triángulo amarillo), lo que nos queda (trapecios rosas) tienen la misma área.

III: Traslación de áreas (trapecios rosas), iguales, no cambia su área.

IV: Si a un área (triángulo verde) le agregamos cosas iguales (trapecios rosas), lo que obtenemos tendrá la misma área (los paralelogramos tendrán la misma área).