Cuadratura de un círculo

«Los geómetras siempre se han esforzado por descubrir las proporciones de las figuras curvilíneas a las rectilíneas y, sin embargo, aún después de emplear el álgebra, esto todavía no es suficiente. Estos problemas no pueden reducirse a ecuaciones algebraicas… el círculo aún no ha podido ser reducido bajo estas leyes de este modo… Porque todavía no se ha encontrado el número que expresa la razón del círculo al cuadrado circunscrito, que es el cuadrado del diámetro».

— G. G. Leibniz

Cuadratura de un círculo

Dado un cuadrado ABCD y un arco BED alrededor del centro A. Y, desplazando la línea AB, de manera que el punto A permanezca fijo y el punto B se desplace a lo largo del arco BED, y la línea BC manteniéndose siempre paralela a la línea AD acompañe al punto B que se mueve a lo largo de la línea AB. Además, el punto B recorra el arco BED en el mismo tiempo que la línea BC recorre la línea BA. Teniendo lugar tal movimiento, las líneas AB, BC, se cortarán entre sí en el punto F y describirá una línea cóncava BFH llamada Cuadratriz de Dinóstrato.

Dado un círculo; se requiere encontrar un cuadrado de la misma área.

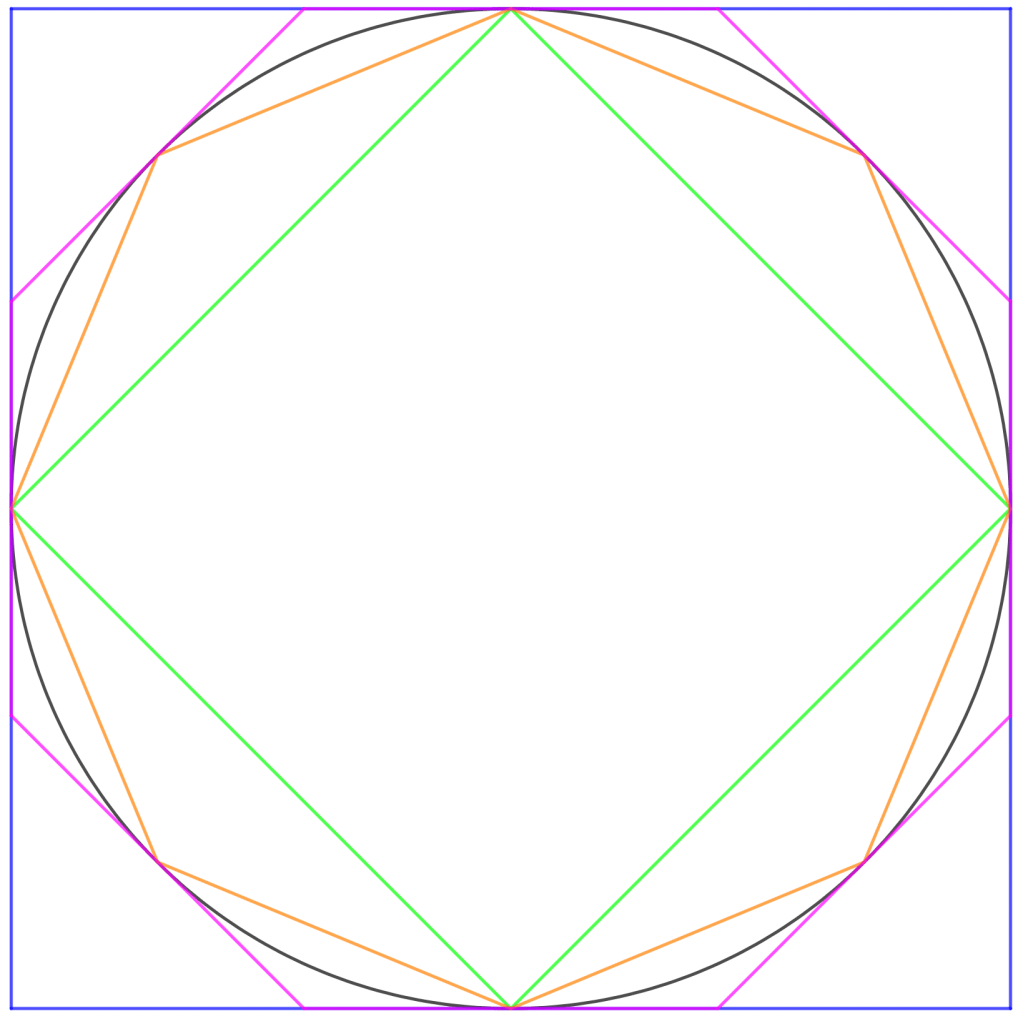
Euclides en los Elementos muestra que podemos inscribir y circunscribir polígonos regulares de lados de manera que la diferencia entre el área del círculo y los polígonos (inscritos y circunscritos) se puede hacer tan pequeña que cualquier área dada (ver Figura-2). Por otro lado, Euclides en los Elementos (libros I y II) describe un método para cuadrar cualquier figura rectilínea en el plano (Ver Método de Aplicación de Áreas). Encuentra un cuadrado equivalente en área a la figura rectilínea dada. De esta forma, tenemos cuadrados de área menor o mayor a la del círculo, si consideramos un polígono inscrito o circunscrito, respectivamente. Entonces, por principio de continuidad para áreas, existe un cuadrado de área igual a la del círculo dado.

Figura-2 Aproximación al área del círculo por polígonos regulares circunscritos e inscritos al mismo.

Ahora bien, todo se reduce a construir el segmento correspondiente al lado del cuadrado buscado. Arquímedes, en el tratado la medida del círculo, reduce el problema de la cuadratura del círculo al problema de encontrar un triángulo rectángulo cuya base es el perímetro del círculo y cuya altura es el radio del mismo. Así, pues, todo se reduce a rectificar la circunferencia, es decir, encontrar un segmento de línea recta equivalente en longitud a la circunferencia del círculo.

Los antiguos griegos encontraron varios procedimientos para rectificar la circunferencia, incluyendo al mismo Arquímedes con su Espiral, uno de ellos, la Cuadratriz de Dinóstrato, cuya propiedad principal por su descripción mecánica (Ver animación) es reducir la proporción de ángulos a la proporción de segmentos rectilíneos: