«Cuando Minos, el mítico rey de Creta, al ver el túmulo levantado en honor a su hijo Glauco, lo encontró demasiado pequeño encargo al arquitecto que lo duplicara… Anduvo buscando entre los geómetras de qué manera sería alguien capaz de duplicar un volumen dado manteniendo la misma forma. Éstos intentaron resolverlo tomando como figura base la de un cubo».
«Los delios fueron a consultar el oráculo de Apolo para librarse de una peste que les aquejaba y recibieron de éste la orden de duplicar el altar».
Duplicación del cubo
La variación continua del punto C sobre la semicircunferencia ABC determina la variación del punto D sobre el segmento AB que, a su vez, determina la variación del punto E cuyo movimiento describe la curva ABE.
Dado un cubo; se requiere encontrar un cubo el doble de volumen del cubo dado.
Dados dos segmentos rectilíneos: a y b, se busca encontrar dos segmentos rectilíneos: x y y, de manera que estén en proporción continua:
De esta forma,
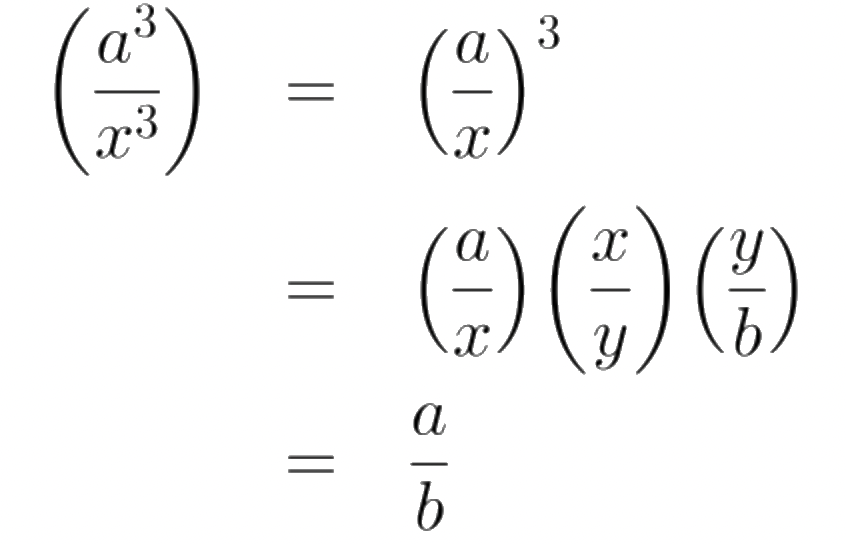
Así pues, 
. Haciendo b=2a, 
. Por otro lado, de la semejanza de los triángulos (ver Figura-1):
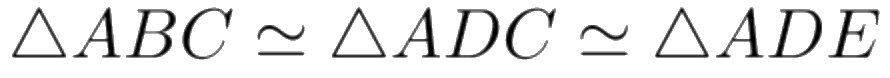
Tenemos:
Haciendo AF=a y AB=b, AC y AD serían dos medias proporcionales, cuando E coincide con F (AE=AF), entre a y b. De esta forma, si C se mueve continuamente sobre la semicircunferencia de diámetro AB, el movimiento de E describe la curva ABE. En suma, resolver el problema de la duplicación del cubo se reduce a determinar cuándo el punto E coincide con F. Ya que la posición del punto C, que determina AC=x -lado del cubo buscado-, depende de la posición de los punto E y D. Ahora bien, si suponemos que conocemos el lugar que ocupa la curva ABE en el plano -conocido en la Antigüedad como lo dado en posición-, es posible determinar cuándo E coincide con F. Así, pues, todo se reduce a determinar AC y AD, conociendo sólo AF y AB. De esta forma, la variación continua que determina a la curva ABE muestra que, existe o es posible, la duplicación del cubo a condición de determinar la posición del punto E cuando éste coincide con F.
Fijo el círculo de diámetro AB=b. El círculo AB’C -de diámetro AB’=AB– girando sobre A, y ortogonal al círculo ABD, describe en su movimiento un toro.
Debemos a Arquitas (428 a. C.-347 a. C.), contemporáneo de Platón, la forma de determinar las dos medias proporcionales: x y y, entre dos segmentos rectilíneos dados: a y b. Es decir, si AF=a y AB=b, Arquitas determina E, de manera que AF=AE (ver Figura-2). Y, por ende, cuando b=2a, tenemos que AC=x es la solución al problema de la duplicación del cubo. Ahora bien, dado a y b, esta determinada la circunferencia de diámetro AB=b, la circunferencia de diámetro AB’=b y la cuerda AF=a (inscrita en la circunferencia ABD). Para determinar E tal que AE=AF -Arquitas- considera la intersección C de dos curvas (ver animación) que, a su vez, una, es la intersección del toro determinado por los círculos ABC y AB’C con el cilindro que determina la rotación del segmento CD sobre la circunferencia ABD (curva amarilla). Otra, la intersección del toro con el cono que determina la rotación del segmento AF sobre el eje AB (curva fiusha). Así, al determinar C queda, también, determinado el punto D que, a su vez, determina al punto E.
israelramos.mx 