Partiendo de que el objetivo de la Geometría es el estudio de las propiedades de las figuras. Lo único que ha cambiado, a través de la historia, es el método con el que se abordan. Así, la finalidad principal de la geometría analítica: recurrir a un sistema de coordenadas para estudiar las propiedades de las figuras en el plano y en el espacio. Análogamente, la geometría diferencial recurre al cálculo diferencial e integral y al álgebra lineal para el estudio de las mismas.

Por otro lado, el objetivo principal de la geometría en la Antigüedad se circunscribió al estudio de la proporción que guardan entre sí las figuras. Respecto al método, unas, recurrieron al principio de continuidad (o principio de divisibilidad infinita). Otras, pudieron evitar, en su argumentación, recurrir al infinito.

Ejemplo de ello, la proporción que guarda la diagonal de un cuadrado con su lado; La proporción que guardan los círculos entre sí (Ver video en Lo insoslayable del infinito en la comprensión de lo finito); La proporción que guardan pirámides de la misma altura y que tienen triángulos como bases; La proporción que guarda la espiral de Arquímedes, en la primera revolución del segmento que la genera, respecto al círculo que, a su vez, se genera por la revolución del mismo (Ver video en Lo insoslayable del infinito en la comprensión de lo finito). En cada una de estas proporciones, para justificar la veracidad de la proporción que se postula, se hace uso del principio de divisibilidad infinita para segmentos, para áreas, para volúmenes y para ángulos, respectivamente.

Ahora bien, el geómetra en la Antigüedad no puede razonar sobre cosas que no existen o no pueden ser exhibidas. Denominado en la jerga euclidiana como lo dado en magnitud, es decir, espacios, líneas y ángulos son dados en magnitud cuando se pueden construir cantidades iguales a éstas. En la Antigüedad, pues, construir es conocer. Pero no todo lo que es posible o existe se puede conocer.

En este sentido, el principio de continuidad subyace a la condición de posibilidad de las cantidades geométricas. Éste permite saber que existe un cuadrado el doble de área de un cuadrado dado; que existe un cubo el doble de volumen de un cubo dado (El problema Délico); que existe la tercera parte de un ángulo dado (Trisección de un ángulo); que existe un cuadrado de área igual a la de un círculo dado (Cuadratura de un círculo). Pero, cómo construyo ese cuadrado; ese cubo; ese ángulo; y ese cuadrado, respectivamente.

En términos de la clasificación dada en la Colección Matemática de Pappus (Siglo IV d. C.), los problemas, en geometría, se clasificaron como planos, sólidos y lineales según se obtengan como la intersección de líneas rectas y circunferencias, como la intersección de cónicas o a través de la intersección de curvas más complejas, respectivamente. 

En los términos anteriores, la duplicación del cubo es posible -existe el lado del cubo buscado-, pero no cognoscible -el segmento de línea recta correspondiente- a través de la intersección de líneas rectas y circunferencias. La cuadratura del círculo: cuadrado de área igual a la de un círculo dado, es posible -existe el lado del cuadrado buscado-, pero no cognoscible a través de la intersección de líneas rectas y circunferencias, así como, tampoco,  a través de la intersección de cónicas.

En suma, la duplicación del cuadrado es un problema de tipo plano, la duplicación del cubo es un problema de tipo sólido y la cuadratura del círculo es un problema de tipo lineal.

Otro ejemplo, a resaltar, es el caso de la construcción del heptágono regular. Kepler observa que existe, es posible pero no cognoscible o construible a través de la intersección de líneas rectas y circunferencias. No es un problema plano. De hecho, es un problema sólido. Ya que la solución se redujo al viejo problema de la trisección de un ángulo que, a su vez, se redujo a encontrar la cuerda que subtiende la tercera parte del ángulo dado. Segmento que se construye como la intersección de una hipérbola con una circunferencia.

En otras palabras, es igualmente posible, si permitimos  no sólo construcciones, mal  nombradas, con regla y compás.

Ahora bien, respecto al viejo problema de la duplicación del cuadrado: Dado un cuadrado, encontrar un cuadrado el doble de área del cuadrado dado. Platón lo aborda en el diálogo del Menón y nos conduce a la solución reduciéndola al cálculo aproximativo del lado del cuadrado a través de saber cómo se modifica el área del cuadrado: 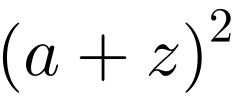, cuando sabemos cómo cambia el lado del mismo: . Otra forma de abordar el problema a través de la teoría de proporciones conducirá a reducir la solución, es decir, cómo conocer el lado de susodicho cuadrado, a la construcción de una media proporcional: x, entre dos segmentos de línea recta  dados: a y b.

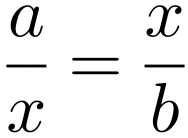
Haciendo b=2a, obtenemos lo solicitado.  A su vez, dicha construcción se realizó a través de la intersección de una circunferencia y una línea recta. Pero el problema de la duplicación del cubo: Dado un cubo, encontrar un cubo el doble de volumen del cubo dado. Como en el caso de la duplicación del cuadrado, la solución se redujo a la construcción de las dos medias  proporcionales: x y y, entre dos segmentos dados: a y b.

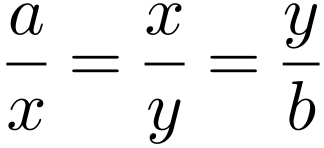
Haciendo b=2a, obtenemos lo solicitado. A diferencia de la inserción de una media proporcional, la de dos medias proporcionales, se realizó a través de la intersección -no de líneas rectas y circunferencias- de dos parábolas o una parábola y una circunferencia (Descartes). 

Y con respecto al problema de la cuadratura de un círculo. Encontrar un cuadrado de área igual a la de un círculo dado. Los geómetras de la Antigüedad sabían que no era posible encontrar la proporción exacta que guardan un círculo y el cuadrado construido sobre su diámetro. Arquímedes redujo el cálculo del área del círculo -dado- al cálculo del área de un triángulo rectángulo cuya base es igual al perímetro del círculo y altura el radio del mismo. Así todo se reduce a rectificar la circunferencia, es decir, encontrar un segmento de línea recta igual -en longitud- a la circunferencia del círculo. De esta forma, la Cuadratriz de Dinóstrato, permite cuadrar un cuarto de círculo toda vez que permite construir un segmento de línea recta de longitud 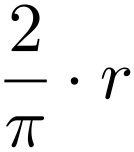. Del cual se puede deducir la construcción del segmento de línea recta de longitud 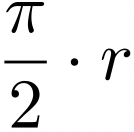, rectificación de una circunferencia asociada a un cuarto de círculo de radio r. Ahora bien, el inconveniente de la descripción mecánica de la cuadratriz es que no es posible conocer más que de forma aproximativa el punto que determina el segmento buscado. Entonces, ¿es posible calcular su valor exacto sin recurrir a aproximaciones cada vez más cercanas?

Arquímedes cálculo que el círculo es aproximadamente 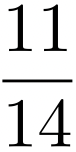del área de su cuadrado circunscrito. Proporción que sabemos es equivalente a calcular el valor de (área de un círculo de diámetro uno). Dicha proporción no es un número racional sino irracional. Lo antes mencionado condujo, a través de la historia, a buscar la ley que gobierna la aproximación infinita de proporciones racionales al número irracional . Su cálculo fue realizado por Leibniz a través de la cuadratura aritmética del círculo:

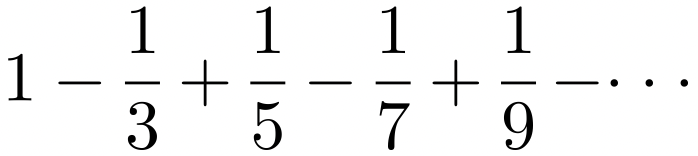
Detrás de la solución asociada a cada uno de los problemas antes mencionados, subyace no solo la posibilidad o existencia del segmento de línea recta buscado sino la construcción correspondiente del mismo. A su vez, esta diferenciación que subyace a toda la tradición clásica de la geometría en la Antigüedad, deviene en una gran variedad de formas -mecánicas- para describir las figuras -curvilíneas- en el plano y en el espacio. Descripciones mecánicas que conjugan diferentes movimientos asociados a variar de forma continua las diferentes cantidades de la geometría. La invariancia que subyace a estas descripciones mecánicas es la condición de posibilidad de la construcción del segmento buscado. Es decir, el conocimiento de la ley o regla que subyace a la variación continua la que determina cómo podemos conocer lo buscado.

Por tanto, no basta apelar a lo infinito, es necesario desvelar su naturaleza -su ley- para aprehenderlo.