Trisección de un ángulo

«Eso que le falto a los matemáticos griegos, son menos los métodos… que las fórmulas propias en la exposición de los métodos».

— Paul Tannery

Trisección de un ángulo

Dado un ángulo inscrito en un rectángulo ABCD; Variando continuamente AC, con A fijo y C variando sobre la prolongación DE de DC, existe un punto E de manera que el ángulo es la tercera parte del ángulo . Es decir, AF divide al ángulo en razón 2:1

Dado un ángulo; se requiere encontrar la tercera parte del ángulo dado.

Se puede suponer sin pérdida de generalidad que el ángulo dado se puede inscribir en un triángulo rectángulo (ver Figura-1). Es decir, cuando el ángulo es obtuso se reduce al caso del ángulo agudo. Así, el principio de variación continua para ángulos, muestra que, si inscribimos el ángulo en un triángulo rectángulo ABC y variamos AC, uno de los lados que determina dicho ángulo, manteniendo fijo A y variando C sobre la prolongación de DC, la inclinación de dicha línea respecto al segmento AB, varia de la inclinación dada -inclinación que forma AE cuando E coincide con C– a inclinación cero -cuando AE es paralela a AB-. De esta forma, en esta variación continua existe una inclinación equivalente a la tercera parte de la inclinación dada.

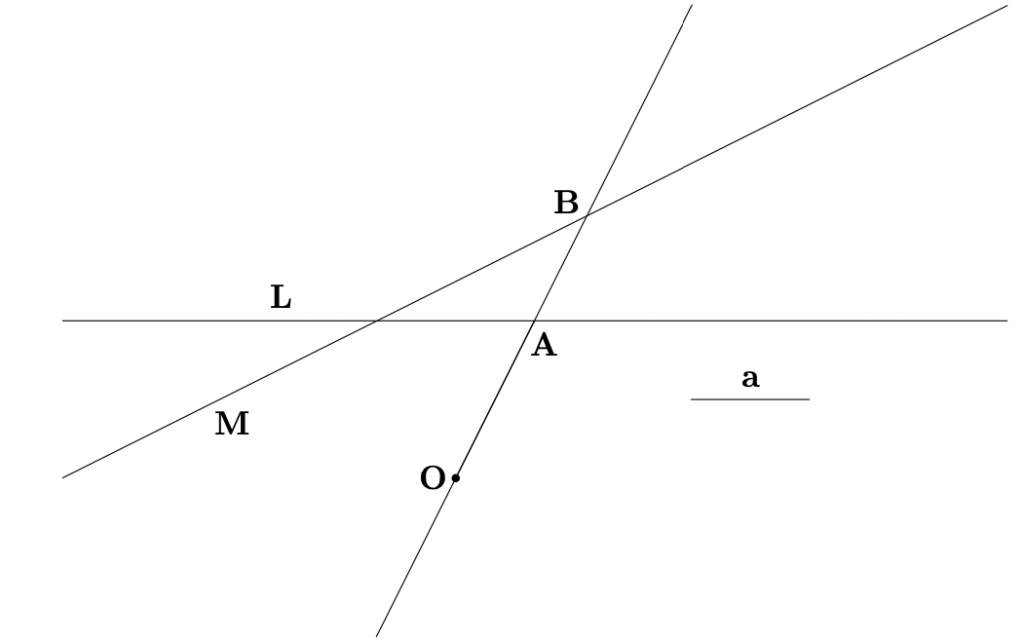
Ahora bien, dentro de esta variación AE esta determinada de forma única, se puede ver que dicha línea cumple que, FE es el doble de AC (ver Figura-1). Así, todo se reduce a, dado un ángulo, , un punto, A, y un segmento, FE, inscribir, desde A, un segmento, sobre los lados que forman el ángulo dado, igual al segmento dado (FE). A este problema en la Antigüedad se le conoció como el problema de Neusis (ver Figura-2), con L y M los lados del ángulo dado, O, el punto dado, y a, el segmento dado; Se busca construir la línea OB de manera que AB=a.

La construcción de dicho segmento se realiza de la siguiente forma. Del punto O se construye un paralelogramo OCDE cuyos lados, OE y OC, son paralelos a las líneas L y M que determinan el ángulo dado (ver animación); Dicho paralelogramo determina una hipérbola CF cuyas asíntotas son las rectas que contienen a los segmentos ED y EO; con centro en C y radio el segmento a, se traza un circunferencia, sea F el punto, que yace en el interior del ángulo dado, de intersección con la hipérbola; trácese una línea paralela a CF por O; Sean A y B, puntos de intersección de ésta con los lados del ángulo dado; se afirma que AB es la línea requerida, es decir, AB=a.