Principio de divisibilidad infinita o sobre el concepto de límite
El concepto de límite, concepto fundamental que subyace al cálculo diferencial e integral, toda vez que, la continuidad, la derivada y la integral, se definen a través de éste. Encuentra su motivación en la Antigüedad con el «cálculo del área del círculo» y el «cálculo del área de la espiral», debido a Euclides y Arquímedes, respectivamente. La necesidad de acompañar el concepto formal de límite con la idea intuitiva del principio de divisibilidad infinita para áreas y del principio de divisibilidad infinita para ángulos que, a su vez, subyacen al cálculo de los dos ejemplos antes mencionados, respectivamente. Objetivo, éste, de nuestro interés para motivar un primer curso de Cálculo Diferencial e Integral.

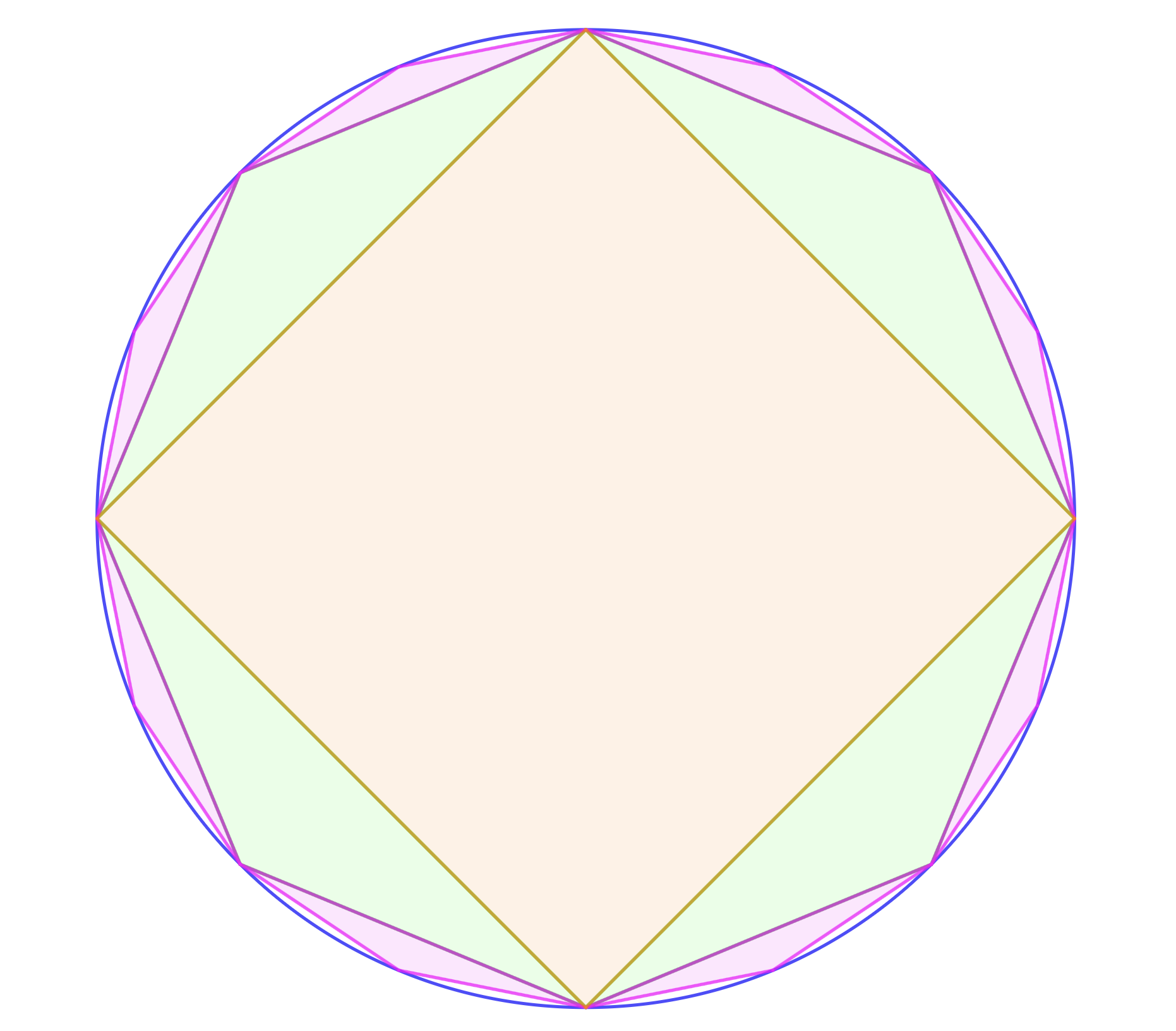
Principio de Divisibilidad Infinita para áreas para calcular el área de un círculo.
