
«El más alto perfeccionamiento que la mente humana puede alcanzar es la aptitud para poder admirar los fenómenos elementales de la naturaleza.»
— J. W. Goethe
En busca de lo absoluto o sobre los principios

La generalidad y la abstracción son rasgos distintivos del quehacer matemático toda vez que, éste, se circunscribió a la búsqueda de la verdad.
El arte de hacer matemáticas consiste en encontrar ese caso especial que contiene todos los gérmenes de generalidad.
David Hilbert
¿Qué es lo que nos ha enseñado a conocer la verdad, las analogías profundas, aquellas que el ojo no ve pero la razón adivina? Es el espíritu matemático, que desdeña la materia para adherirse a la forma pura. Esto es lo que nos ha enseñado a dar el mismo nombre a cosas difiriendo sólo materialmente.
Henri Poincaré
El camino de la verdad es largo, sin embargo, existe una forma sistemática de abordarla. En este sentido, la Antigüedad, distinguió entre el arte de descubrimiento de la verdad y el arte de exposición de la verdad.
Puesto el fin, consideran cómo y por qué medios pueden alcanzarlo; y si parece que el fin puede ser alcanzado por varios medios, examinan cuál es el más fácil y mejor, y si no hay más que uno para lograrlo, cómo se logrará a través de éste, y éste, a su vez, mediante cuál otro, hasta llegar a la causa primera que es la última en el descubrimiento… y lo último en el análisis es lo primero en la génesis.
Ética Nicomáquea – Ética Eudemia, Aristóteles
Para fijar ideas, supongamos que nos solicitan demostrar la veracidad de la proposición P1 y, para ello, deducimos como consecuencia de lo que nos fue dado: P1, las proposiciones P2, P3, hasta Pn, pero, Pn es una proposición conocida o deducible de mi conjunto de axiomas, definiciones y postulados. El camino de P1 a Pn:
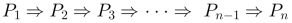
desvela el análisis que nos permite dar cuenta cómo podemos deducir la veracidad de P1 de una proposición conocida Pn que, a su vez, puede ser deducida de nuestro conjunto de axiomas, definiciones y postulados. El camino inverso,

puede no siempre existir pero cuando éste existe nos permite demostrar la veracidad de la proposición P1. Encontrar las condiciones que posibilitan el camino inverso es equivalente en general a saber cuándo la implicación inversa de una implicación es cierta:
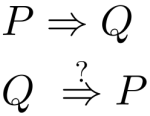
El camino de P1 a Pn se conoció, en la Antigüedad, como el método del análisis, es decir, suponiendo la veracidad de la proposición que quiero demostrar, P1, qué otras propiedades puedo deducir de este hecho o hipótesis, y de éstas cuál es ya conocida o deducible de mis supuestos: axiomas, definiciones y postulados. El camino de Pn a P1, se conoció como el arte de exposición de la verdad (o síntesis), respecto al arte de descubrimiento de la verdad, el método del análisis jugo un papel importante en desvelar no la verdad sino el cómo corroborarla, es el principio de variación continua (ver Geometría Sintética) la heurística que les permitió, a los antiguos, circunscribirse al arte de descubrimiento de la verdad.
Ahora bien, el esquema de la síntesis:

nos permite reparar en los atributos principales que subyacen a todo quehacer matemático, a saber, la generalidad y la abstracción. Supongamos que Pn no es una proposición conocida sino un principio, axioma, definición o postulado. Conocer el alcance de un axioma, definición o postulado nos permite generalidad.
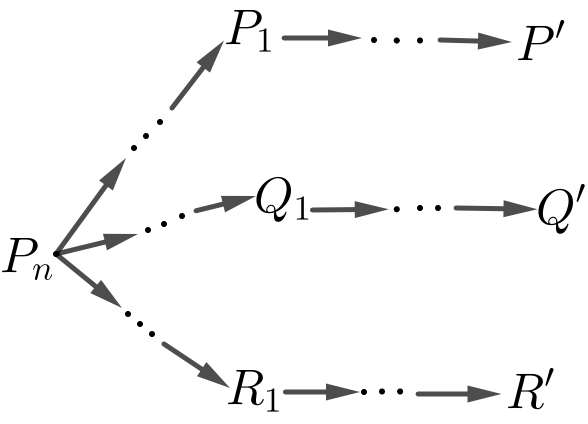
Me explico, supongamos que Pn es el quinto postulado de la geometría euclidiana:
Postulado 5. Y que si una recta al incidir sobre dos rectas hace los ángulos internos del mismo lado menores que dos rectos [180°], las dos rectas prolongadas indefinidamente se encontrarán en el lado en el que están los (ángulos) menores que dos rectos.
Elementos, Euclides.
Analizar el alcance del quinto postulado nos permite saber qué propiedades de las figuras dependen del mismo y que, al mismo tiempo, nos permitiría saber que éstas no valdrían en geometrías no-euclidianas (o independientes del quinto postulado). O, en su defecto, nos permitiría saber qué propiedades son propias de la geometría absoluta, es decir, valdrían en cualquier geometría.
Por ejemplo, si P’ es la proposición que afirma que el ángulo inscrito en una circunferencia que subtiende un arco de semicircunferencia es de 90°, depende del quinto postulado (Pn);
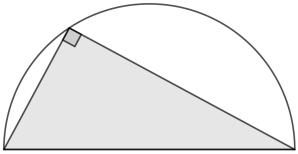
si Q’ es la proposición que afirma que la suma de los ángulos interiores de un triangulo es 2R (180°), depende del quinto postulado (Pn); si R’ es la proposición que afirma que las líneas rectas paralelas son equidistantes, depende del quinto postulado (Pn).
De esta forma, en una geometría independiente del quinto postulado, podríamos preguntarnos, ¿cuánto vale el ángulo inscrito en una circunferencia que subtiende un arco de semicircunferencia?; ¿cuánto valen la suma de los ángulos interiores de un triángulo?; ¿cuál el comportamiento de las líneas paralelas?, más aún, ¿existen las paralelas?
Por otro lado, la abstracción, nos permite profundizar en el sentido y significado de nuestros axiomas, definiciones o postulados.
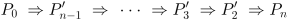
Para fijar ideas, supongamos que Pn es la definición XI.10 de los Elementos de Euclides que reza
Definición 10. Las figuras sólidas iguales son aquellas que están contenidas por planos iguales [y situados de manera similar], iguales en número y magnitud.
Elementos, XI. Euclides [Herón].
Esta definición euclidiana recoge un criterio para saber cuándo dos figuras sólidas rectilíneas [convexas] son congruentes (y, por ende, del mismo volumen). Esta definición se consideró un teorema, es decir, deducible de nuestros axiomas, definiciones y postulados de la geometría plana y sólida toda vez que, una propiedad análoga en el plano, criterios de congruencia de triángulos son teoremas (salvo el criterio de congruencia Lado-Angulo-Lado que, prácticamente, Hilbert axiomatiza en Foundations of Geometry. ¿Por qué?). Entonces, ¿por qué este criterio de congruencia para sólidos rectilíneos [convexos] tendría que tener el estatus de una definición? ¿Por qué no se demuestra por el método de superposición como el caso de los criterios de congruencia para triángulos?
La demostración de este hecho depende de varias propiedades acerca de los polígonos convexos y de los ángulos sólidos. Propiedades que hacen referencia no a una propiedad de magnitud sino a una propiedad topológica. De entre ellas, podríamos resaltar el invariante de Euler:
Teorema. En un poliedro convexo, se cumple
V-A+C=2,
donde V, denota el número de vértices; A, el número de aristas y C, el número de caras.
Lo cual tienen como consecuencia las siguientes observaciones:
Teorema [Cauchy, 1813]. En un poliedro convexo cuyas caras son todas invariantes, los vértices comprendidos entre las caras o, lo que es lo mismo, las inclinaciones en las distintas aristas son también invariantes; de modo que, con las mismas caras, solo se puede construir un segundo poliedro convexo simétrico al primero.
Corolario. Dos poliedros convexos, incluidos bajo el mismo número de caras iguales y colocadas de manera similar, son superponibles o simétricos y, en ambos casos, son necesariamente iguales.
De esta forma, Cauchy hace descansar la demostración de la definición XI.10 de los Elementos de Euclides en una serie de proposiciones, P’2, P’3, … , P’n-1, asociadas a polígonos convexos y ángulos sólidos, y a la proposición, P0, asociada al invariante de Euler (Teorema de Euler antes citado).
Ahora bien, en el plano se pueden construir dos polígonos convexos de cuatro lados de la misma longitud, no simétricos y no superponibles:
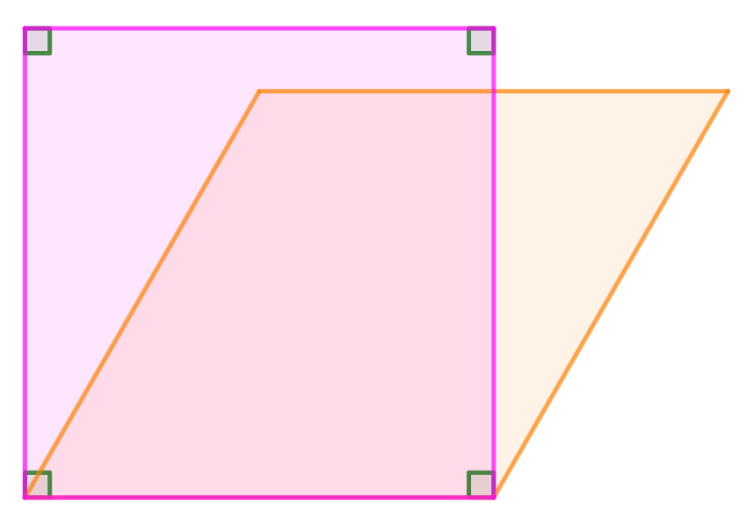
Lo cual nos invita a reflexionar acerca de la naturaleza del espacio, toda vez que, la observación análoga en el espacio no sucede por Teorema de Cauchy.
Ahora supongamos que P0 es el método de exhaución y P1, la proposición que a la letra dice
Proposición. Las pirámides que tienen la misma altura y tienen triángulos como bases son entre sí como sus bases.
Elementos, XII.5. Euclides
Lo que estamos observando es que el cálculo del volumen de una pirámide depende del método de exhaución. ¿Podemos demostrar P1 sin hacer uso del método de exhaución? Detrás de la respuesta a esta pregunta subyace nuestra comprensión de la naturaleza del espacio, ya que la propiedad análoga en el plano, a saber,
Proposición. Los triángulos que tienen la misma altura […] son entre sí como sus bases.
Elementos, VI.1. Euclides
Es independiente del método de exhaución. La pregunta equivalente, en analogía con el procedimiento que conduce a la demostración de la pregunta análoga en el plano y que no usa el método de exhaución sino los procedimientos de equidescomposición y equicomplementariedad (ver Cálculo del área en la Antigüedad), reza
Problema [Tres de Hilbert, 1900]. Dados dos tetraedros de igual volumen, ¿es siempre posible cortar el primero en una cantidad finita de piezas tetraédricas que puedan ser ensambladas de modo que quede armado el segundo?
La respuesta es no. En suma, lo insoslayable del infinito en el espacio para el cálculo del volumen de una pirámide, a diferencia del plano donde el cálculo del área de un triángulo soslaya el infinito. Nos invita a reflexionar acerca de la naturaleza del espacio; el cálculo del volumen para sólidos rectilíneos [convexos] conduce a desvelar propiedades topologícas, en el plano y en el espacio, de las que depende este cálculo, lo cual nos invita a conjeturar si, en general, ¿el cálculo de las magnitudes: longitud, área y volumen se puede reconstruir por las propiedades no de magnitud sino de posición, es decir, de propiedades topologícas?
Supongamos, ahora, que P1 es el quinto postulado, es decir, buscamos demostrar el quinto postulado. Empresa que, por ejemplo, emprendió Girolamo Sacceri, jesuita del siglo XVII, sin éxito. El quinto postulado se considero un teorema y no un postulado por lo controversial de su planteamiento. Me explico, consideremos dos líneas, l1 y l2, y una transversal, l3, que hace ángulos internos del mismo lado iguales a un recto (90°).
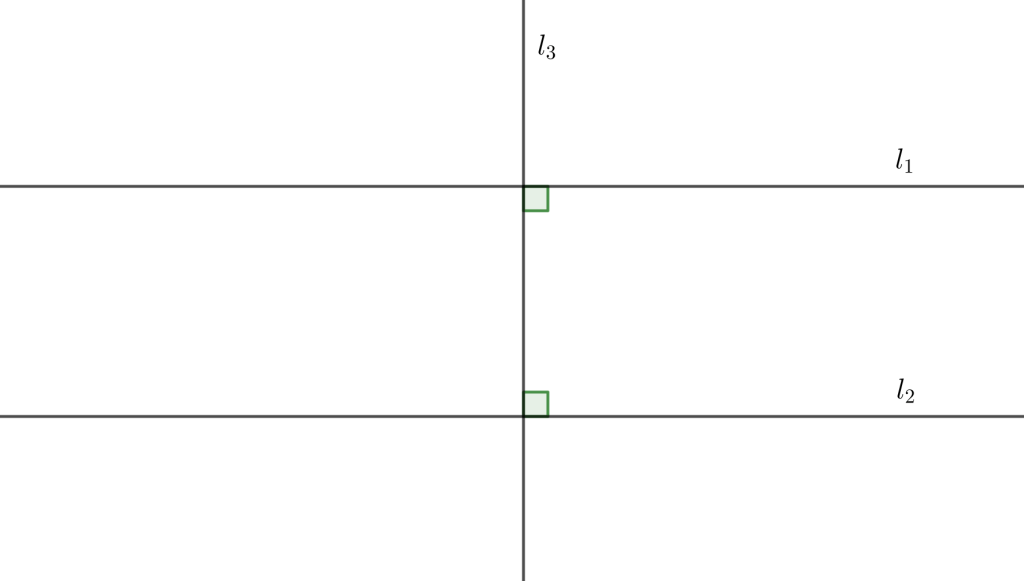
Se puede intuir que el comportamiento de l1 y l2 respecto a uno u otro lado de l3 es el mismo, es decir, que si l1 y l2 se cortan de un lado se tendrían que cortar del otro lado pero dos líneas rectas no pueden cortarse en más de un punto (equivalentemente, dos líneas rectas no pueden encerrar espacio). Así pues, dada la naturaleza de una línea recta, l1 y l2 tendrían necesariamente que ser paralelas, es decir, que al prolongarse indefinidamente de uno u otro lado de l3 nunca se cortan. Ahora bien, supongamos que l3 es ortogonal a l2 y con l1 hace un ángulo agudo, de manera que la suma de los ángulos internos del mismo lado es menor a 2R (180°).
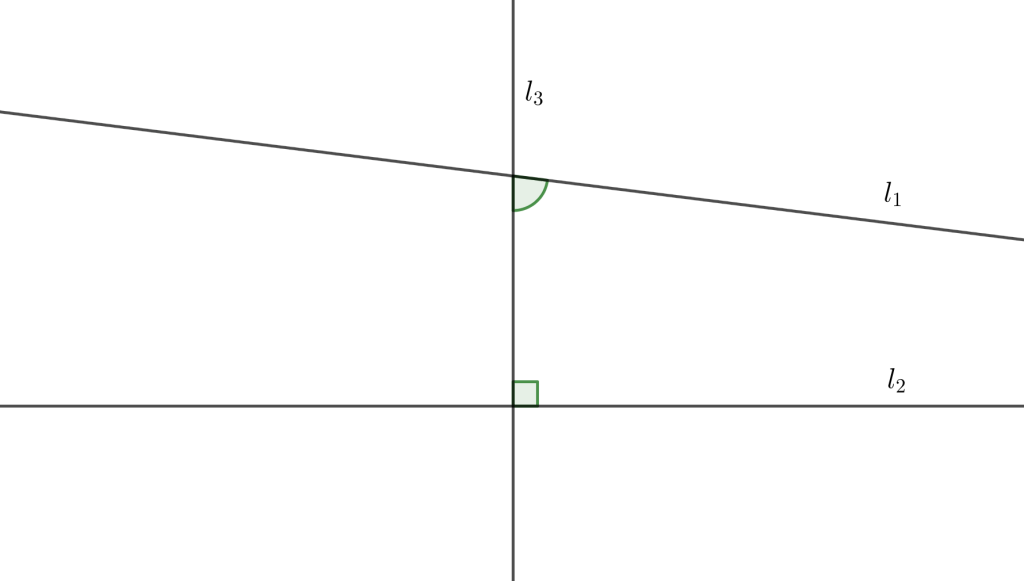
Entonces, ¿l1 y l2 se cortan?, ¿de qué lado se cortan? ¿Por qué la respuesta a estas preguntas tendrían que tener la evidencia de un axioma?
Por otro lado, por qué lo que le sucede a una hipérbola, l1, respecto a su asíntota, l2, no tendría que suceder cuando l1 y l2 son dos líneas rectas, a saber, incidiendo l3 con l1 y l2, y hacer ángulos internos del mismo lado menores que 2R, l1 y l2 no se cortan.
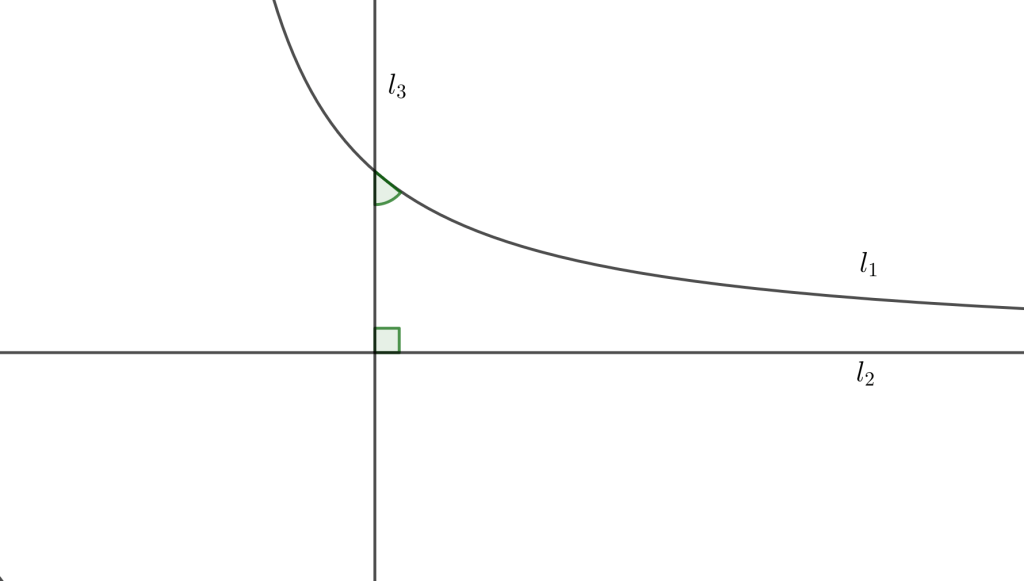
En suma, la distinción fundamental que subyace al quinto postulado, a saber, línea recta y línea curva no tiene la evidencia de un axioma. Consideremos dos hipérbolas simétricas, l1 y l2, respecto a la perpendicular común l3. Y, sin embargo, l1 y l2 no se cortan.

Qué de mis axiomas, definiciones y postulados (excepto el quinto), incluyendo mi definición de línea recta que a letra dice,
Definición 4. Una línea recta es aquella que yace por igual respecto de los puntos que están en ella
Elementos, Euclides.
Nos permite excluir el comportamiento de los casos , l1 hipérbola y l2 línea recta, y, l1 y l2 hipérbolas. En otras palabras, qué hace que una línea recta sea recta (o se vaya derecha). Qué, supuesto o hipótesis, determina la naturaleza de una línea recta toda vez que el concepto de línea curva como aquella en la que ninguna parte es recta, es claro, toda vez que el concepto de línea recta lo sea, pero el concepto de línea recta, según su definición, es poco claro o incompleto si nos circunscribimos al hecho de que la característica principal, dos líneas rectas no encierran espacio, no esta justificado en el contexto euclidiano:
axiomas, definiciones y postulados, y de las consecuencias que de ello puedo deducir, es decir, de los trece libros que constituyen los Elementos de Euclides.
Ahora bien, no obstante que Girolamo Sacceri en, Euclides vindicatus, demuestra erróneamente el quinto postulado, podemos rescatar observaciones que son correctas y que desvelan la hipótesis que subyace a la naturaleza de los tres tipos de geometría a las que dan nacimiento, a saber, la geometría euclidiana, la geometría hiperbólica y la geometría elíptica, respectivamente:
- Hipótesis del ángulo recto
- Hipótesis del ángulo agudo
- Hipótesis del ángulo obtuso
Si sobre un segmento tomado como base se levantan en los extremos dos ortogonales de la misma longitud y trazamos la línea que une los extremos de éstas, entonces los ángulos de la tapa de dicho cuadrilátero son siempre iguales, independientemente del quinto postulado, así existen tres posibilidades:
- Los ángulos de la tapa son rectos
- Los ángulos de la tapa son agudos
- Los ángulos de la tapa son obtusos
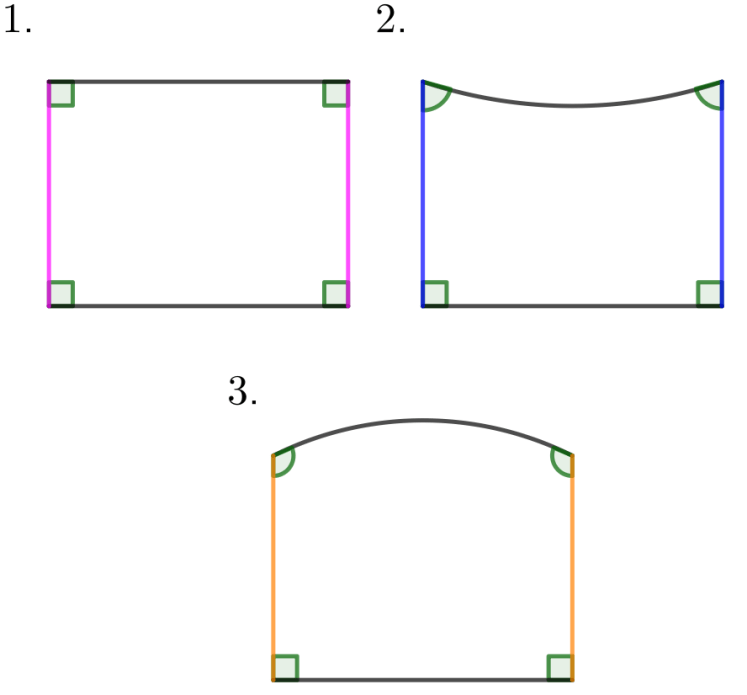
El primer caso, es la hipótesis del ángulo recto; el segundo, la hipótesis del ángulo agudo y el tercero, la hipótesis del ángulo obtuso.
De esta forma,
El cuadrilátero de Sacceri contiene los gérmenes de generalidad.
Toda vez que, de éste, se deduce el comportamiento de las líneas que conforman la tapa de este cuadrilátero y, por ende, se deduce la existencia o no de líneas paralelas en cada hipótesis y el comportamiento de las mismas que, a su vez, determinan las propiedades de las figuras en cada geometría.
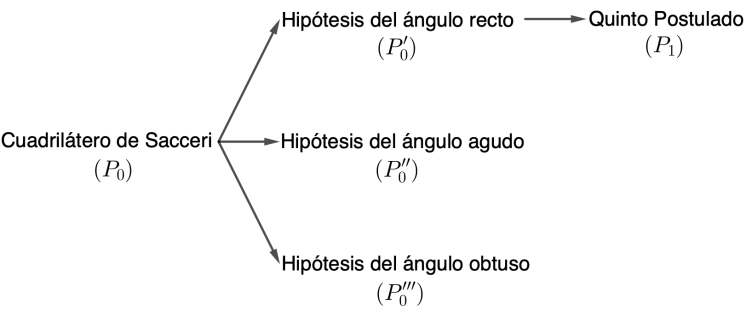
En suma, profundizar en el planteamiento del quinto postulado, equivalentemente, profundizar en el concepto de línea paralela conduce a desvelar la propiedad de la geometría absoluta que subyace a la emergencia de nuevas geometrías.
Supongamos que, P0, es el axioma que postula la construcción de una línea recta que pasa por dos puntos dados y la construcción de una circunferencia que tiene como centro un punto dado y radio un segmento dado. Analizar el alcance de los problemas de la geometría que pueden resolverse como la intersección de líneas rectas y circunferencias conduce a desvelar la naturaleza que subyace a las propiedades de las figuras en el plano y en el espacio. Me doy a entender, podemos afirmar con conocimiento de causa que, si nos circunscribimos al objetivo general de la geometría antigua, a saber, el estudio de la proporción que guardan entre sí las figuras, la propiedad que subyace al cálculo del área de las figuras rectilíneas y curvilíneas en el plano, es la construcción de la media y tercera proporcional, x, entre dos segmentos de línea recta dados: a y b,
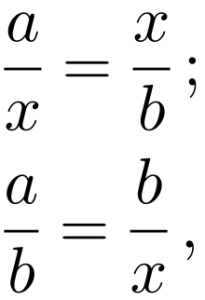
que, a su vez, se pueden construir como la intersección de una línea recta y una circunferencia. Equivalentemente, cuadrar un rectángulo,
x2=ab,
es decir, encontrar el lado, x, de un cuadrado de área igual a la de un rectángulo dado, ab; encontrar la altura, x, de un rectángulo de base dada, a, de área igual a la de un cuadrado dado:
ax=b2.
Para fijar ideas, veamos cómo Euclides, en la Antigüedad, cálculo implícitamente el área de un círculo, y digo implícitamente, ya que no lo calcula a través de la fórmula conocida sino comparando ésta con el área de otro círculo, es decir, lo que Euclides calculó fue la proporción que guardan entre sí cualesquiera dos círculos:
Proposición. Los círculos son uno a otro como los cuadrados de sus diámetros.
Elementos, XII.2. Euclides
Medir, en la Antigüedad, es comparar. Ya que no había unidad de medida en la geometría. A diferencia de la aritmética. La introducción de una unidad se hará aproximadamente 2000 años después por René Descartes en su libro La Geometrie. Y, no obstante ello, los grandes geómetras de la Antigüedad calcularon el área de la superficie de la esfera, el volumen de la esfera, el área de un sector de parábola, la longitud de la circunferencia, etcétera. Así, pues, existe un concepto primigenio del concepto moderno de medida: longitud, área y volumen.
Ahora bien, hagamos un esbozo de las ideas que subyacen a la demostración de la Proposición XII.2:
- De la Proposición VI.1, Los triángulos que tienen la misma altura […] son entre sí como sus bases, y suponiendo que AD, es la tercera proporcional entre AB y A’B’: AB/A’B’=A’B’/AD. Se sigue la siguiente afirmación:
Proposición. Los triángulos semejantes guardan entre sí la razón duplicada de sus lados correspondientes.
Elementos, VI.19. Euclides.
En efecto, de la hipótesis sobre AD, se tiene:
AB2/A’B’2=AB/AD.
Por otro lado, si construimos un triángulo cuya base sea AD y de la misma altura que el triángulo ABC (ver Figura), por Proposición VI.1, Área( ABC)/Área(ADC)=AB/AD.

Así, Área( ABC)/Área(ADC)=(AB)2/(A’B’)2. Además, afirmamos que, Área( ADC)=Área(A’B’C‘). En efecto, por hipótesis, ABC es semejante a A’B’C’, entonces
AB/A’B’=AC/A’C’.
Así
A’C’/A’B’=AC/AB.
Y, también,
AB/A’B’=A’B’/AD.
Así
A’B’/AD=AC/A’C’.
Por tanto, los lados de los triángulos, A’B’C’ y ADC, están inversamente relacionados respecto a ángulos iguales, C’A’B’ y CAD. De esta forma, por
Proposición. […] Y aquellos triángulos que tienen un ángulo (de uno) igual a un ángulo (del otro) cuyos lados que comprende los ángulos iguales están inversamente relacionados, son iguales [tienen la misma área].
Elementos, VI.15. Euclides.
Los triángulos A’B’C‘ y ADC tienen la misma área. Por lo tanto, del hecho
Área( ABC)/Área(ADC)=(AB)2/(A’B’)2,
y Área(ADC)=Área(A‘B’C’), tenemos
Área( ABC)/Área(A’B’C’)=(AB)2/(A’B’)2.
- De la observación anterior, Proposición VI.19, se sigue el siguiente hecho más general:
Proposición. Los polígonos semejantes se dividen en triángulos semejantes e iguales en número y homólogos a los (polígonos) enteros y un polígono guarda con el otro una razón duplicada de la que guarda el lado correspondiente con el lado correspondiente.
Elementos, VI.20. Euclides

- Del cual, a su vez, se sigue la siguiente propiedad:
Proposición. Los polígonos semejantes inscritos en círculos son uno a otro como los cuadrados de los diámetros.
Elementos, XII.1. Euclides
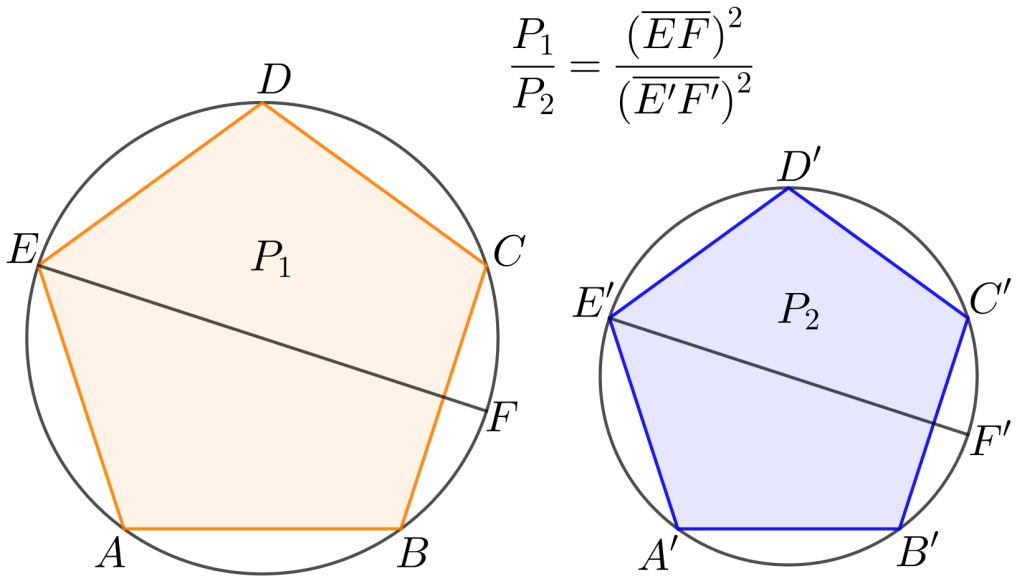
- Proposición XII.1+Método de Exhaución, implica XII.2. Q. E. D. (Quod Erat Demostrandum).
Las observaciones antes mencionadas nos conducen a una generalización del Teorema de Pitágoras (ver Generalización del Teorema de Pitágoras para otra generalización basada en los métodos de equidescomposición y equicomplementariedad de figuras).
Proposición [Generalización del Teorema de Pitágoras]. En los triángulos rectángulos, la figura (construida) a partir del lado que subtiende el ángulo recto es igual a las figuras semejantes y construidas de manera semejante a partir de los lados que comprenden el ángulo recto.
Elementos, VI.31. Euclides.
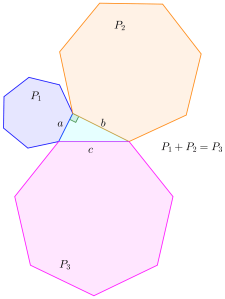
En efecto, por Proposición VI.20,
P1/P3=a2/c2
y
P2/P3=b2/c2.
Así
P1/P3+P2/P3=a2/c2+b2/c2.
De esta forma,
(P1+P2)/P3=(a2+b2)/c2.
Por tanto,
(P1+P2)/P3=1,
ya que a2+b2=c2. Es decir,
P1+P2=P3.
Análogamente, la propiedad que subyace al cálculo del volumen de los sólidos rectilíneos y curvilíneos en el espacio, es la construcción de la inserción de dos medias, x y y, entre dos segmentos de línea recta dados: a y b,
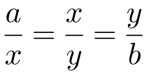
Equivalentemente,
a3/x3=a/b,
es decir,
x3=a2b.
La construcción de la inserción de dos medias no se puede realizar a través de la intersección de líneas rectas y circunferencias, sin embargo, si postulamos la construcción de una parábola, entonces ésta se pude realizar como la intersección de dos parábolas (Al-Khayyām) o como la intersección de una parábola con una circunferencia (Descartes):
Para el caso particular, b=2a, ver El problema Délico.
En general, en la Antigüedad, la práctica de resolución de problemas conduce a los antiguos a llevar a cabo la descripción mecánica (o construcción) de diferentes curvas: concoide, cisoide, cuadratriz, espiral, hipérbola, elipse, etcétera (ver Geometría Sintética; Trisección de un ángulo; Cuadratura de un círculo; Conferencias: Gauss y el Teorema Fundamental del Álgebra, primera parte), que permiten resolver los problemas que se plantearon: El problema de Neusis (ver Trisección de un ángulo) con la concoide; la inserción de dos medias proporcionales y duplicación del cubo con la cisoide; cuadratura del círculo con la cuadratriz; rectificación de la circunferencia y trisección de un ángulo con la espiral de Arquímedes; trisección de un ángulo con la hipérbola y circunferencia; etcétera.
En fin… no es vano detenerse en el ejercicio de analizar el papel del método axiomático en nuestra intuición lógica del espacio.
