Método de Aplicación de Áreas

«Estas cosas, según Eudemo, son antiguas y fueron invención de la Musa de los pitagóricos, quiero decir la aplicación de áreas por yuxtaposición, por exceso y por defecto. Los geómetras posteriores tomaron estas denominaciones de los pitagóricos y las trasladaron a las líneas llamadas cónicas, de modo que una de ellas nombra la parábola, otra la hipérbola y otra la elipse, mientras que los hombres de la Antigüedad, semejantes a dioses, veían que estos términos significaban la construcción de áreas, en el plano, sobre una línea recta finita»

— Proclo

Las cónicas como aplicación de áreas

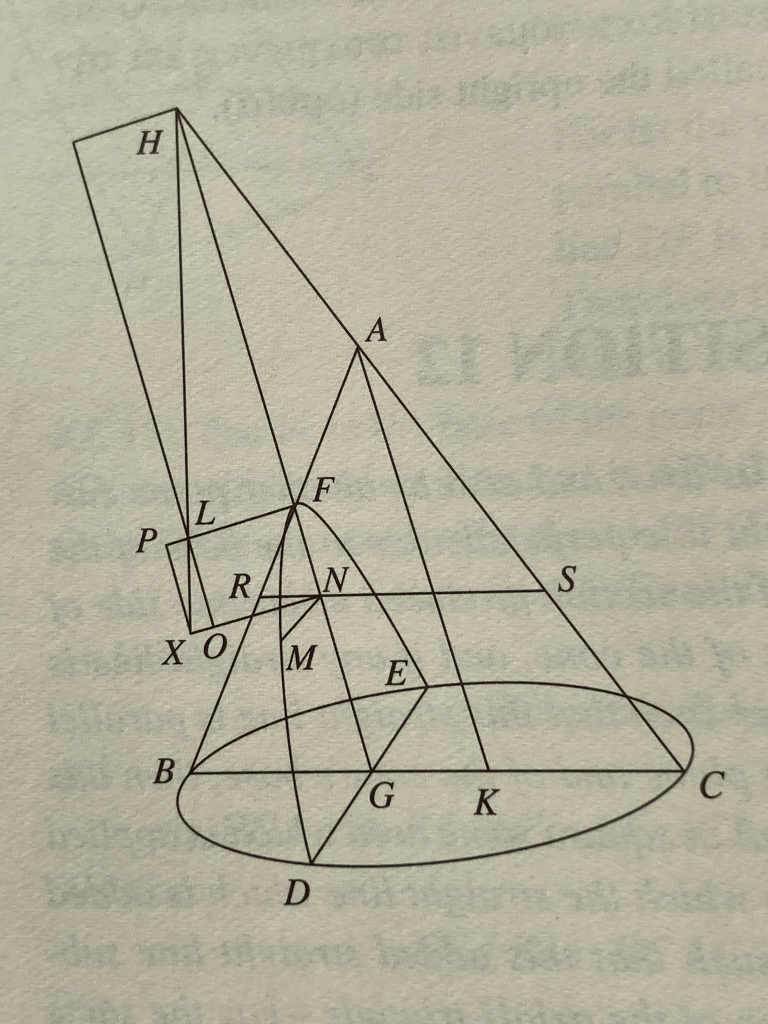
El cálculo del área en el plano, en la Antigüedad, se circunscribió al problema general de la cuadratura de cualquier figura. Sea ésta rectilínea o curvilínea. Es decir, encontrar un cuadrado equivalente en área a una figura dada. Consideremos el caso de cualquier figura rectilínea. Triangulando la figura y encontrando un paralelogramo por cada elemento de la triangulación cuyos lados sean paralelos a un ángulo dado y equivalente en área a dicho elemento (ver Animación: Triangulación figura rectilínea; Cálculo del área en la Antigüedad).

Triangulación figura rectilínea.

Basta con encontrar un método para sumar cualesquiera dos paralelogramos y, de esta forma, encontrar un paralelogramo equivalente en área a la figura dada. Ahora bien, dado que el ángulo dado (agudo y de color rojo) que determina el primer paralelogramo puede ser diferente al ángulo dado (recto y de color azul) que determina al segundo paralelogramo (ver Animación: Triangulación figura rectilínea). El método de aplicación de áreas encuentra su origen en desarrollar un método que nos permita sumar dos paralelogramos (color naranja y color azul, respectivamente) determinados por cualesquiera dos ángulos dados, encontrando, dos paralelogramos, equivalentes en área a los paralelogramos color naranja y azul, respectivamente, pero cuyos lados sean paralelos a un ángulo común (color rojo, ver Animación).

Paralelogramos con ángulo común dado equivalente en área a dos paralelogramos dados.

Por otro lado, teniendo dos paralelogramos, color naranja y color azul, cuyos lados son paralelos a un ángulo común, puede suceder que, no compartan, ahora, un lado común para poder pegar ambos paralelogramos a través de dicho lado.

Suma de dos paralelogramos con ángulo común dado.

Así, pues, se requiere, dado un segmento (color verde), un ángulo (color rojo) y un paralelogramo (color naranja), encontrar un paralelogramo cuyos lados sean paralelos a los lados del ángulo dado, cuya base sea el lado dado y equivalente en área al paralelogramo dado (ver Figura: Aplicación de área por yuxtaposición).

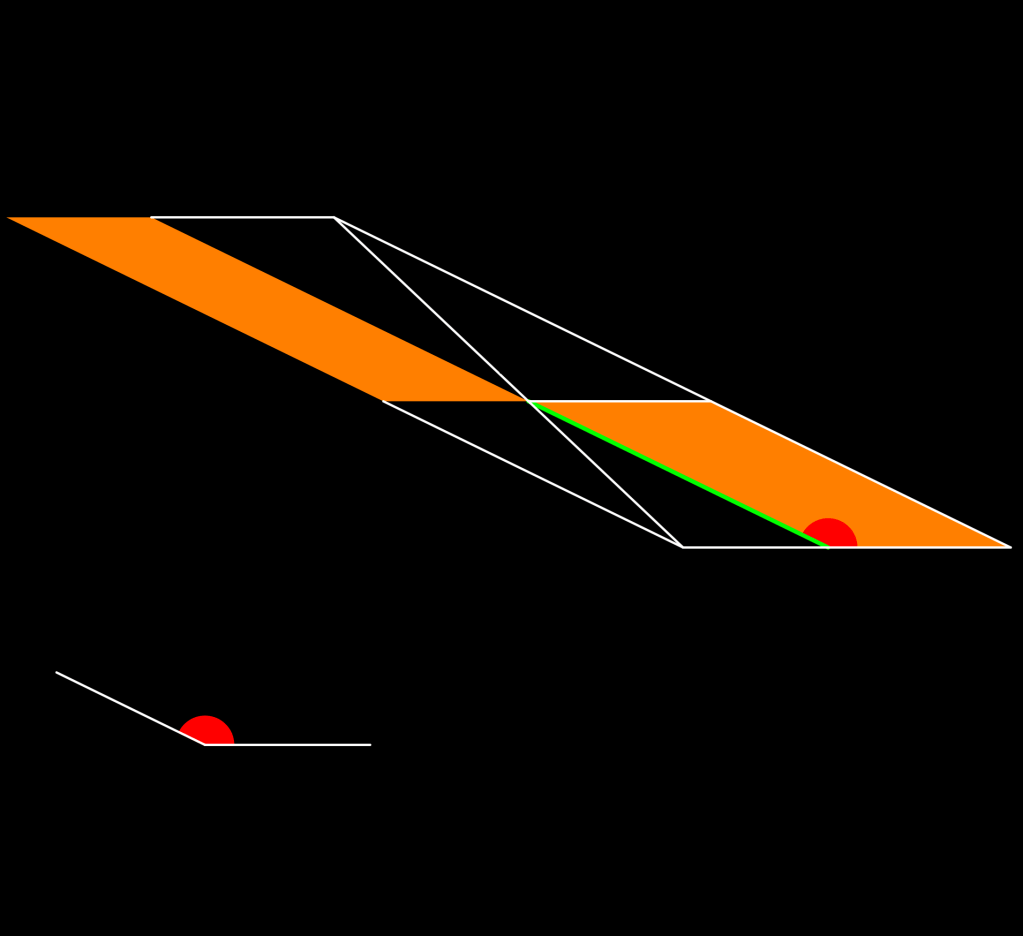
Cuando el ángulo dado es un ángulo recto, el paralelogramo dado se convierte en un rectángulo.

En suma, cuadrar cualquier figura rectilínea es equivalente a cuadrar cualquier rectángulo. De esta forma, si consideramos un rectángulo dado de base PB y altura PD. Y, con diámetro AB (AP=PD), trazamos una circunferencia, y ortogonal en P, consideramos el segmento PE. Entonces, por potencia interior de un punto P respecto a una circunferencia, se cumple que el cuadrado construido sobre PE es igual en área al rectángulo dado (color amarillo, ver Figura: Cuadratura de un rectángulo).

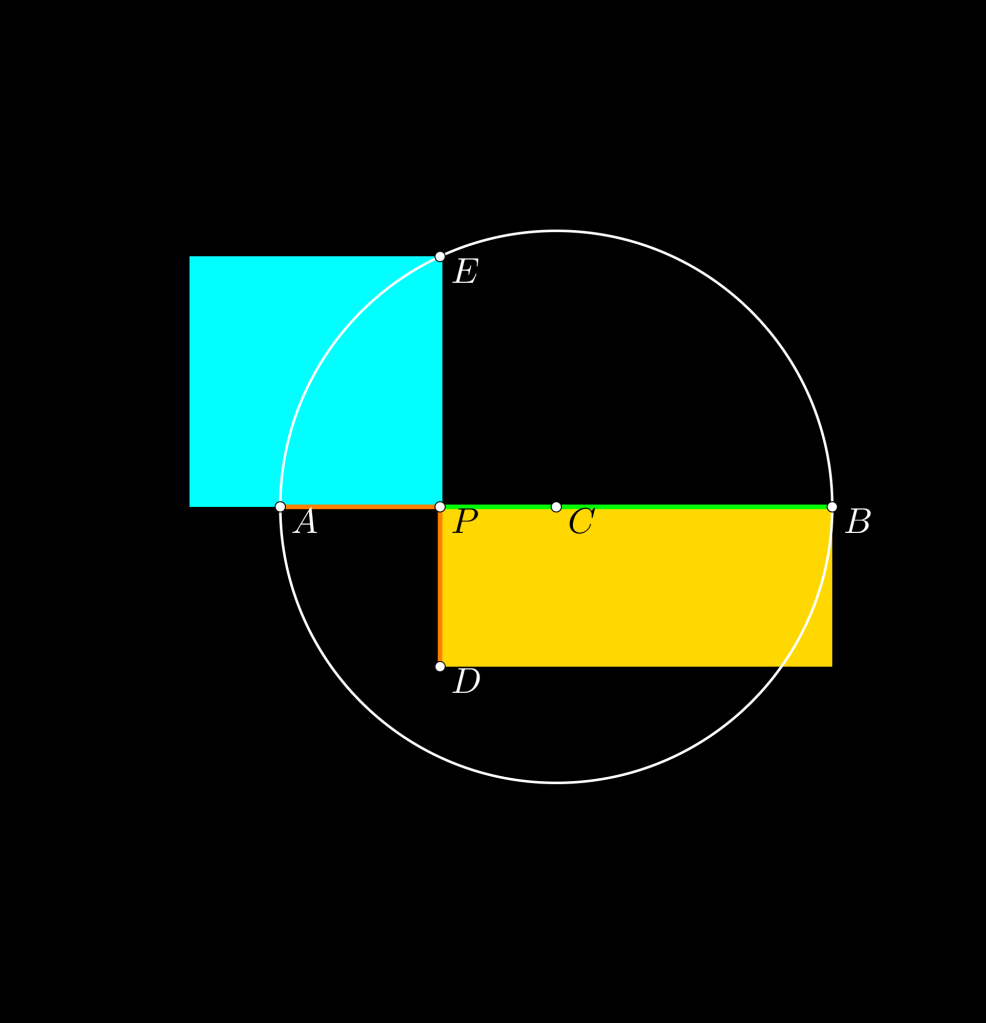
Ahora bien, si nos es dado un segmento (color rojo) y un área rectilínea (que podemos suponer sin perdida de generalidad que es un cuadrado cuyo lado es color fiusha), el método de aplicación del área dada –cuando ésta varia de forma continua– sobre el segmento dado –y fijo– por yuxtaposición, genera una rama de una parábola (ver Animación).

Aplicación de áreas por yuxtaposición.

Por otro lado, si nos es dado un segmento (color rojo) y un área rectilínea (que podemos suponer sin perdida de generalidad que es un cuadrado cuyo lado es color fiusha), el método de aplicación del área dada –cuando ésta varia de forma continua– sobre el segmento dado –y fijo– y que excede en un cuadrado de lado x (color amarillo), genera una rama de una hipérbola (ver Animación).

Aplicación de áreas por exceso.

Pero, si nos es dado un segmento (color rojo) y un área rectilínea (que podemos suponer sin perdida de generalidad que es un cuadrado cuyo lado es color fiusha), el método de aplicación del área dada –cuando ésta varia de forma continua– sobre el segmento dado –y fijo– y que es deficiente en un cuadrado de lado x (color amarillo), genera un arco de circunferencia (ver Animación).

Aplicación de áreas por defecto.

O, si nos es dado un segmento (color rojo) y un paralelogramo equivalente a una área dada, el método de aplicación del área dada –cuando ésta varia de forma continua– sobre el segmento dado –y fijo– y que es deficiente en un paralelogramo semejante al paralelogramo dado, genera un arco de elipse (ver Animación).

Aplicación de áreas por defecto.