Historia de los números complejos en tres actos
Sobre el origen de los números complejos
Respecto a la construcción o representación geométrica de los números complejos, no se sabe por qué, éstos, se representan con la parte imaginaria ortogonal a la parte real. En este sentido, el matemático inglés John Wallis (1616-1703) fue el primero en hacer una contribución importante a la representación de los mismos, ya que muestra una representación diferente a la que hoy día tenemos en la que la parte imaginaria no es ortogonal a la parte real. Esto marca la pauta para preguntarnos, ¿por qué elegimos la representación en la que la parte imaginaria es ortogonal a la parte real, y no elegimos la representación
geométrica dada por Wallis? Esta pregunta presupone, a su vez, que hay otra representación: la que hoy día tenemos de los números complejos. ¿Esta representación proviene de algún problema de naturaleza geométrica? El problema sobre la representación de los números complejos se puede dividir en tres actos: El primero, la imposibilidad de darle un sentido geométrico. Segundo, los intentos de darle un sentido geométrico. Y tercero, acerca de la compatiblidad de su cálculo con su correspondiente representación geométrica.
Sobre los números imaginarios que surgen en la resolución de la ecuación x3+B=Ax
Para conocer lo real hay que pasar por lo complejo
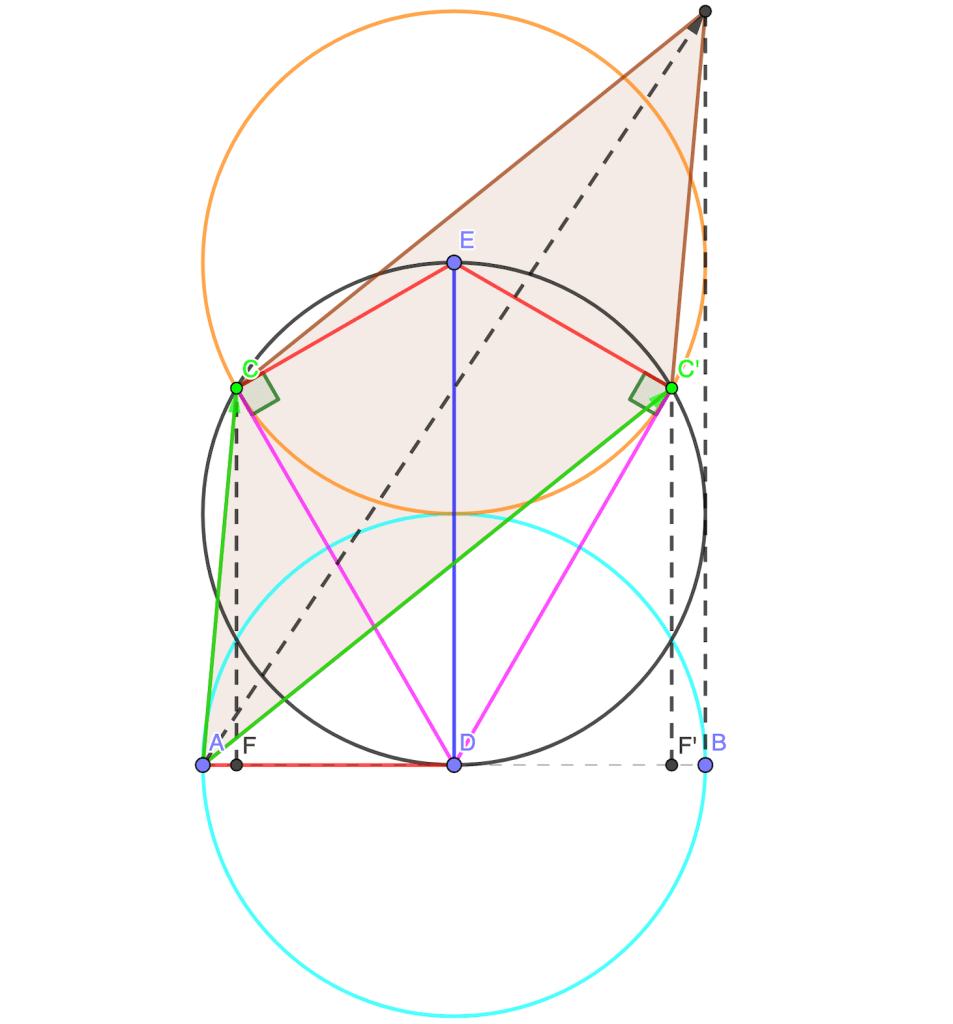
Dada la representación de las raíces complejas de la ecuación x2+b2=ax dada por John Wallis (1673) en la que la parte real e imaginaria no son ortogonales, como lo representamos hoy día, se puede observar que si bien, Wallis, no puede darle sentido a la suma de números complejos conjugados, asociados a las raíces de la ecuación cuadrática antes mencionada, cuya suma es a. Wallis muestra que las proyecciones de éstas –proyección de C y C’— al segmento AB (como se muestra en la figura), sí suman a (longitud del segmento AB). De esta forma, si consideramos el paralelogramo que forman estas raíces, AB coincide con la proyección de la diagonal sobre el segmento AB. Es decir, la representación geométrica de los números complejos, dada por Wallis, no es compatible con el cálculo de los mismos como expresiones algebraicas en las que se multiplican o suman como si multiplicase o sumase números reales salvo que (√-1)2=-1. ¿Existe una representación de los números complejos cuyo cálculo sea compatible con su representación geométrica? En 1637 René Descartes lleva la solución del viejo problema de la
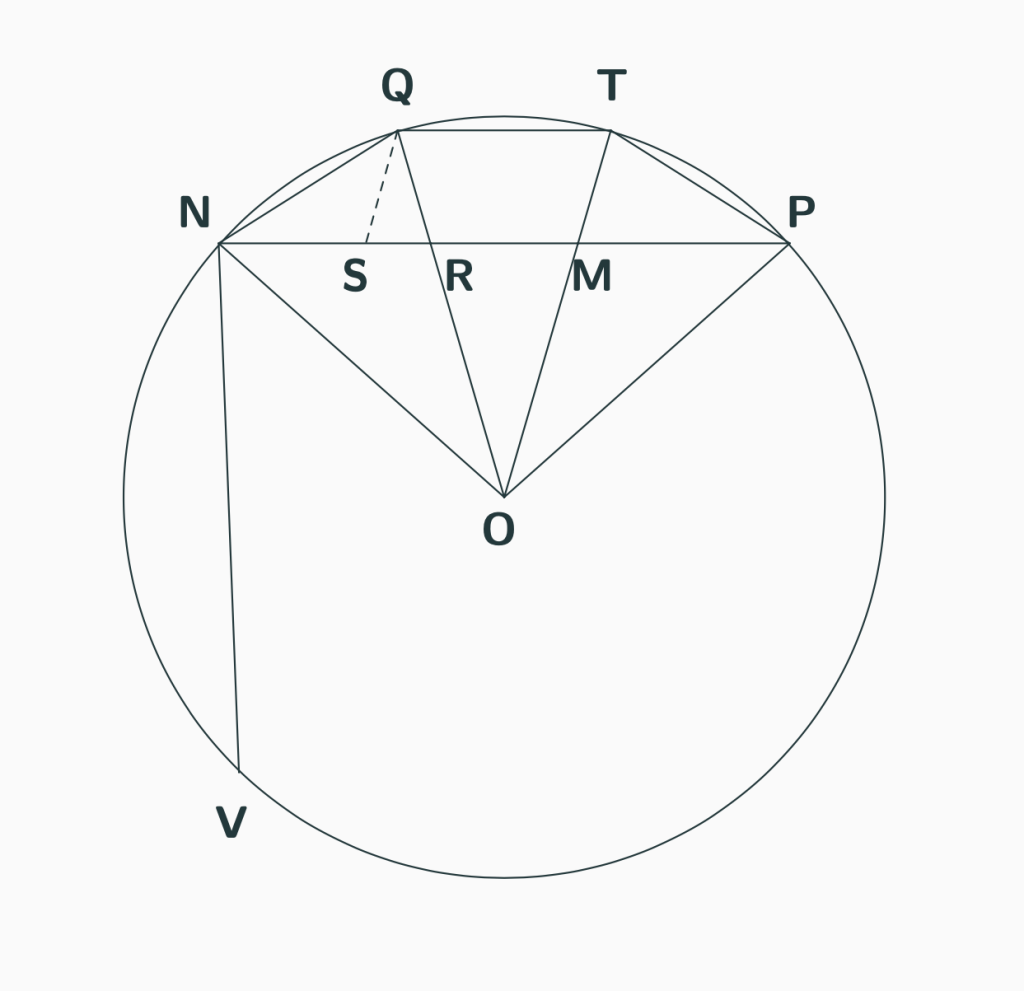
trisección de un ángulo (ver figura) a la solución de la ecuación cúbica x3+qr2=3r2x, donde q es la cuerda NP que determina el ángulo NOP a trisecar, r radio del círculo donde se inscribe el ángulo a trisecar y x (NQ o NV) la cuerda que subtiende la tercera parte del ángulo dado. Cuando q<2r, el problema tiene dos soluciones reales y, por ende, tres raíces reales. Ésta tercera raíz negativo de la suma de las otras dos, raíz positiva de la ecuación x3=Ax+B, aplicando las fórmulas Cardano para la misma, resulta que la condición para que esta ecuación tenga soluciones reales es, q>2r, haciendo A=3r2, B=qr2. ¿Dónde yace el absurdo? Equivalentemente, para que en la fórmula de Cardano que expresa la solución real de la ecuación cúbica aparezcan números complejos es, q<2r, así pues la raíz real se expresa, según las fórmulas de Cardano, como la suma de dos números complejos conjugados. ¿Existe un problema de naturaleza geométrica asociado a esta tercera raíz como el caso de las otras dos raíces asociadas a la trisección de ángulos conjugados?
Naturaleza del logaritmo de los números negativos
Controversia Leibniz&Bernoulli
Cálculo del área en la Antigüedad
Equidescomposición
En la Antigüedad, la falta de una unidad en la geometría condujo a los geómetras a medir a través de comparar cantidades de la misma naturaleza (cantidades homogéneas). De esta forma, la equidescomposición: descomponer una figura en figuras menores y reordenarlas para formar otra figura de la misma área; y la equicomplementariedad: agregar figuras (de la misma área) a una figura dada para formar dos figuras de la misma área, fueron dos procedimientos que permitieron mostrar que, si a iguales les quitamos cosas iguales, lo que nos queda son cosas iguales. Si a iguales les agregamos cosas iguales, lo que resulta son cosas iguales. Así, pues, estos dos métodos permitieron a Euclides mostrar:
Paralelogramos de la misma base y entre las mismas paralelas son iguales entre sí (paralelogramos que tienen la misma base y alturas iguales, tienen la misma área).
Lo anterior sin determinar una fórmula para el cálculo del área de un paralelogramo, ya que no había una unidad de medida.
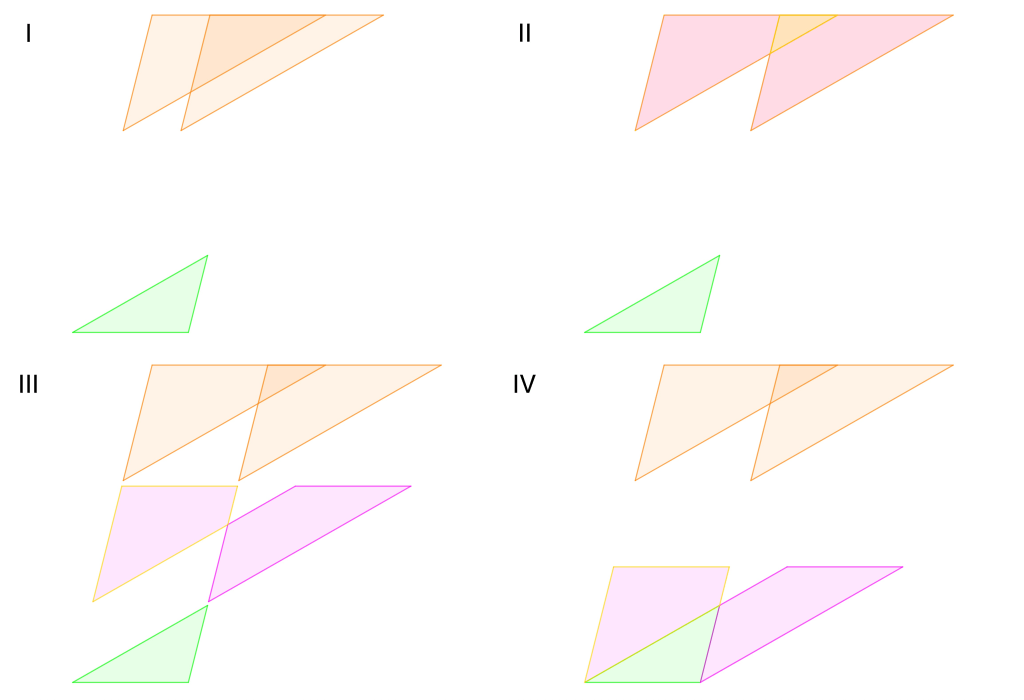
De izquierda a derecha y de arriba a abajo (ver la figura):
I: Traslación de un triángulo (pintado de naranja) no cambia su área.
II: Si a áreas iguales (triángulos naranjas) substraemos una misma área (triángulo amarillo), lo que nos queda (trapecios rosas) tienen la misma área.
III: Traslación de áreas (trapecios rosas), iguales, no cambia su área.
IV: Si a un área (triángulo verde) le agregamos cosas iguales (trapecios rosas), lo que obtenemos tendrá la misma área (los paralelogramos tendrán la misma área).
Generalización del Teorema de Pitágoras
Teorema de Pitágoras
En la Antigüedad, Euclides desarrollo un método para cuadrar cualquier figura rectilínea dada. Un método para encontrar un cuadrado igual en área a la de cualquier figura rectilínea dada (ver Método de Aplicación de Áreas). Detrás de este método, «el arte de soldar cuadrados», yace el descubrimiento de una propiedad geométrica que cumplen todos los triángulos rectángulos: el Teorema de Pitágoras. Y, a su vez, detrás de la veracidad de esta propiedad geométrica yace el antiguo método de la aplicación de áreas, método que conjugado con el arte de la analogía nos permite saber: a condición de qué la propiedad geométrica de los triángulos rectángulos -Teorema de Pitágoras- se puede extender a cualquier triángulo.
Geometría Sintética
En busca del infinito
Partiendo de que el objetivo de la Geometría es el estudio de las propiedades de las figuras. Lo único que ha cambiado, a través de la historia, es el método con el que se abordan. Así, la finalidad principal de la geometría analítica: recurrir a un sistema de coordenadas para estudiar las propiedades de las figuras en el plano y en el espacio. Análogamente, la geometría diferencial recurre al cálculo diferencial e integral y al álgebra lineal para el estudio de las mismas.
Por otro lado, el objetivo principal de la geometría en la Antigüedad se circunscribió al estudio de la proporción que guardan entre sí las figuras. Respecto al método, unas, recurrieron al principio de continuidad (o principio de divisibilidad infinita). Otras, pudieron evitar, en su argumentación, recurrir al infinito.
Ejemplo de ello, la proporción que guarda la diagonal de un cuadrado con su lado; La proporción que guardan los círculos entre sí; La proporción que guardan pirámides de la misma altura y que tienen triángulos como bases; La proporción que guarda la espiral de Arquímedes, en la primera revolución del segmento que la genera, respecto al círculo que, a su vez, se genera por la revolución del mismo. En cada una de estas proporciones, para justificar la veracidad de la proporción que se postula, se hace uso del principio de divisibilidad infinita para segmentos, para áreas, para volúmenes y para ángulos, respectivamente.
Ahora bien, el geómetra en la Antigüedad no puede razonar sobre cosas que no existen o no pueden ser exhibidas. Denominado en la jerga euclidiana como lo dado en magnitud, es decir, espacios, líneas y ángulos son dados en magnitud cuando se pueden construir cantidades iguales a éstas. En la Antigüedad, pues, construir es conocer. Pero no todo lo que es posible o existe se puede conocer.
En este sentido, el principio de continuidad subyace a la condición de posibilidad de las cantidades geométricas. Éste permite saber que existe un cuadrado el doble de área de un cuadrado dado; que existe un cubo el doble de volumen de un cubo dado (El problema Délico); que existe la tercera parte de un ángulo dado (Trisección de un ángulo); que existe un cuadrado de área igual a la de un círculo dado (Cuadratura de un círculo). Pero, cómo construyo ese cuadrado; ese cubo; ese ángulo; y ese cuadrado, respectivamente.
En términos de la clasificación dada en la Colección Matemática de Pappus (Siglo IV d. C.), los problemas, en geometría, se clasificaron como planos, sólidos y lineales según se obtengan como la intersección de líneas rectas y circunferencias, como la intersección de cónicas o a través de la intersección de curvas más complejas, respectivamente.
En los términos anteriores, la duplicación del cubo es posible -existe el lado del cubo buscado-, pero no cognoscible -el segmento de línea recta correspondiente- a través de la intersección de líneas rectas y circunferencias. La cuadratura del círculo: cuadrado de área igual a la de un círculo dado, es posible -existe el lado del cuadrado buscado-, pero no cognoscible a través de la intersección de líneas rectas y circunferencias, así como, tampoco, a través de la intersección de cónicas.
En suma, la duplicación del cuadrado es un problema de tipo plano, la duplicación del cubo es un problema de tipo sólido y la cuadratura del círculo es un problema de tipo lineal.
Otro ejemplo, a resaltar, es el caso de la construcción del heptágono regular. Kepler observa que existe, es posible pero no cognoscible o construible a través de la intersección de líneas rectas y circunferencias. No es un problema plano. De hecho, es un problema sólido. Ya que la solución se redujo al viejo problema de la trisección de un ángulo que, a su vez, se redujo a encontrar la cuerda que subtiende la tercera parte del ángulo dado. Segmento que se construye como la intersección de una hipérbola con una circunferencia.
En otras palabras, es igualmente posible, si permitimos no sólo construcciones, mal nombradas, con regla y compás.
Ahora bien, respecto al viejo problema de la duplicación del cuadrado: Dado un cuadrado, encontrar un cuadrado el doble de área del cuadrado dado. Platón lo aborda en el diálogo del Menón y nos conduce a la solución reduciéndola al cálculo aproximativo del lado del cuadrado a través de saber cómo se modifica el área del cuadrado: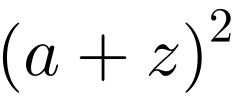 
, cuando sabemos cómo cambia el lado del mismo: 
. Otra forma de abordar el problema a través de la teoría de proporciones conducirá a reducir la solución, es decir, cómo conocer el lado de susodicho cuadrado, a la construcción de una media proporcional: x, entre dos segmentos de línea recta dados: a y b.
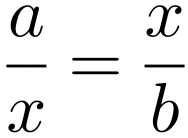
Haciendo b=2a, obtenemos lo solicitado. A su vez, dicha construcción se realizó a través de la intersección de una circunferencia y una línea recta. Pero el problema de la duplicación del cubo: Dado un cubo, encontrar un cubo el doble de volumen del cubo dado. Como en el caso de la duplicación del cuadrado, la solución se redujo a la construcción de las dos medias proporcionales: x y y, entre dos segmentos dados: a y b.
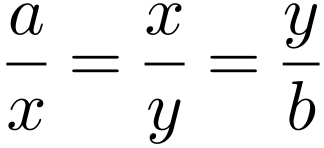
Haciendo b=2a, obtenemos lo solicitado. A diferencia de la inserción de una media proporcional, la de dos medias proporcionales, se realizó a través de la intersección -no de líneas rectas y circunferencias- de dos parábolas o una parábola y una circunferencia (Descartes).
Y con respecto al problema de la cuadratura de un círculo. Encontrar un cuadrado de área igual a la de un círculo dado. Los geómetras de la Antigüedad sabían que no era posible encontrar la proporción exacta que guardan un círculo y el cuadrado construido sobre su diámetro. Arquímedes redujo el cálculo del área del círculo -dado- al cálculo del área de un triángulo rectángulo cuya base es igual al perímetro del círculo y altura el radio del mismo. Así todo se reduce a rectificar la circunferencia, es decir, encontrar un segmento de línea recta igual -en longitud- a la circunferencia del círculo. De esta forma, la Cuadratriz de Dinóstrato, permite cuadrar un cuarto de círculo toda vez que permite construir un segmento de línea recta de longitud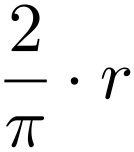 
. Del cual se puede deducir la construcción del segmento de línea recta de longitud 
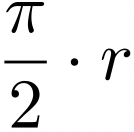, rectificación de una circunferencia asociada a un cuarto de círculo de radio r. Ahora bien, el inconveniente de la descripción mecánica de la cuadratriz es que no es posible conocer más que de forma aproximativa el punto que determina el segmento buscado. Entonces, ¿es posible calcular su valor exacto sin recurrir a aproximaciones cada vez más cercanas?
Arquímedes cálculo que el círculo es aproximadamente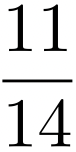 
del área de su cuadrado circunscrito. Proporción que sabemos es equivalente a calcular el valor de 
(área de un círculo de diámetro uno). Dicha proporción no es un número racional sino irracional. Lo antes mencionado condujo, a través de la historia, a buscar la ley que gobierna la aproximación infinita de proporciones racionales al número irracional . Su cálculo fue realizado por Leibniz a través de la cuadratura aritmética del círculo:
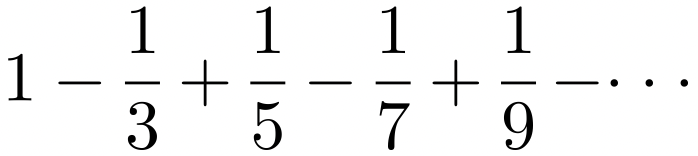
Detrás de la solución asociada a cada uno de los problemas antes mencionados, subyace no solo la posibilidad o existencia del segmento de línea recta buscado sino la construcción correspondiente del mismo. A su vez, esta diferenciación que subyace a toda la tradición clásica de la geometría en la Antigüedad, deviene en una gran variedad de formas -mecánicas- para describir las figuras -curvilíneas- en el plano y en el espacio. Descripciones mecánicas que conjugan diferentes movimientos asociados a variar de forma continua las diferentes cantidades de la geometría. La invariancia que subyace a estas descripciones mecánicas es la condición de posibilidad de la construcción del segmento buscado. Es decir, el conocimiento de la ley o regla que subyace a la variación continua la que determina cómo podemos conocer lo buscado.
Por tanto, no basta apelar a lo infinito, es necesario desvelar su naturaleza -su ley- para aprehenderlo.
Duplicación del cubo
La variación continua del punto C sobre la semicircunferencia ABC determina la variación del punto D sobre el segmento AB que, a su vez, determina la variación del punto E cuyo movimiento describe la curva ABE.
Dado un cubo; se requiere encontrar un cubo el doble de volumen del cubo dado.
Dados dos segmentos rectilíneos: a y b, se busca encontrar dos segmentos rectilíneos: x y y, de manera que estén en proporción continua:
De esta forma,
Así pues, 
. Haciendo b=2a, 
. Por otro lado, de la semejanza de los triángulos (ver Figura-1):
Tenemos:
Haciendo AF=a y AB=b, AC y AD serían dos medias proporcionales, cuando E coincide con F (AE=AF), entre a y b. De esta forma, si C se mueve continuamente sobre la semicircunferencia de diámetro AB, el movimiento de E describe la curva ABE. En suma, resolver el problema de la duplicación del cubo se reduce a determinar cuándo el punto E coincide con F. Ya que la posición del punto C, que determina AC=x -lado del cubo buscado-, depende de la posición de los punto E y D. Ahora bien, si suponemos que conocemos el lugar que ocupa la curva ABE en el plano -conocido en la Antigüedad como lo dado en posición-, es posible determinar cuándo E coincide con F. Así, pues, todo se reduce a determinar AC y AD, conociendo sólo AF y AB. De esta forma, la variación continua que determina a la curva ABE muestra que, existe o es posible, la duplicación del cubo a condición de determinar la posición del punto E cuando éste coincide con F.
Fijo el círculo de diámetro AB=b. El círculo AB’C -de diámetro AB’=AB– girando sobre A, y ortogonal al círculo ABD, describe en su movimiento un toro.
Debemos a Arquitas (428 a. C.-347 a. C.), contemporáneo de Platón, la forma de determinar las dos medias proporcionales: x y y, entre dos segmentos rectilíneos dados: a y b. Es decir, si AF=a y AB=b, Arquitas determina E, de manera que AF=AE (ver Figura-2). Y, por ende, cuando b=2a, tenemos que AC=x es la solución al problema de la duplicación del cubo. Ahora bien, dado a y b, esta determinada la circunferencia de diámetro AB=b, la circunferencia de diámetro AB’=b y la cuerda AF=a (inscrita en la circunferencia ABD). Para determinar E tal que AE=AF -Arquitas- considera la intersección C de dos curvas (ver animación) que, a su vez, una, es la intersección del toro determinado por los círculos ABC y AB’C con el cilindro que determina la rotación del segmento CD sobre la circunferencia ABD (curva amarilla). Otra, la intersección del toro con el cono que determina la rotación del segmento AF sobre el eje AB (curva fiusha). Así, al determinar C queda, también, determinado el punto D que, a su vez, determina al punto E.
Trisección de un ángulo
Dado un ángulo 
inscrito en un rectángulo ABCD; Variando continuamente AC, con A fijo y C variando sobre la prolongación DE de DC, existe un punto E de manera que el ángulo 
es la tercera parte del ángulo . Es decir, AF divide al ángulo en razón 2:1
Dado un ángulo; se requiere encontrar la tercera parte del ángulo dado.
Se puede suponer sin pérdida de generalidad que el ángulo dado se puede inscribir en un triángulo rectángulo (ver Figura-1). Es decir, cuando el ángulo es obtuso se reduce al caso del ángulo agudo. Así, el principio de variación continua para ángulos, muestra que, si inscribimos el ángulo en un triángulo rectángulo ABC y variamos AC, uno de los lados que determina dicho ángulo, manteniendo fijo A y variando C sobre la prolongación de DC, la inclinación de dicha línea respecto al segmento AB, varia de la inclinación dada -inclinación que forma AE cuando E coincide con C– a inclinación cero -cuando AE es paralela a AB-. De esta forma, en esta variación continua existe una inclinación equivalente a la tercera parte de la inclinación dada.
Ahora bien, dentro de esta variación AE esta determinada de forma única, se puede ver que dicha línea cumple que, FE es el doble de AC (ver Figura-1). Así, todo se reduce a, dado un ángulo, 
, un punto, A, y un segmento, FE, inscribir, desde A, un segmento, sobre los lados que forman el ángulo dado, igual al segmento dado (FE). A este problema en la Antigüedad se le conoció como el problema de Neusis (ver Figura-2), con L y M los lados del ángulo dado, O, el punto dado, y a, el segmento dado; Se busca construir la línea OB de manera que AB=a.
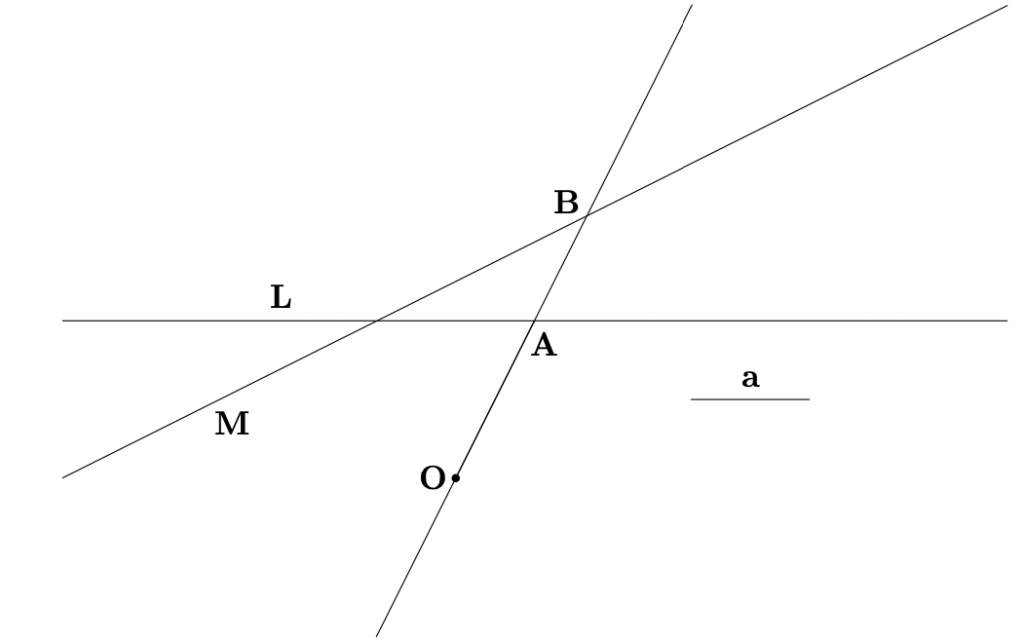
La construcción de dicho segmento se realiza de la siguiente forma. Del punto O se construye un paralelogramo OCDE cuyos lados, OE y OC, son paralelos a las líneas L y M que determinan el ángulo dado (ver animación); Dicho paralelogramo determina una hipérbola CF cuyas asíntotas son las rectas que contienen a los segmentos ED y EO; con centro en C y radio el segmento a, se traza un circunferencia, sea F el punto, que yace en el interior del ángulo dado, de intersección con la hipérbola; trácese una línea paralela a CF por O; Sean A y B, puntos de intersección de ésta con los lados del ángulo dado; se afirma que AB es la línea requerida, es decir, AB=a.
Cuadratura de un círculo
Dado un cuadrado ABCD y un arco BED alrededor del centro A. Y, desplazando la línea AB, de manera que el punto A permanezca fijo y el punto B se desplace a lo largo del arco BED, y la línea BC manteniéndose siempre paralela a la línea AD acompañe al punto B que se mueve a lo largo de la línea AB. Además, el punto B recorra el arco BED en el mismo tiempo que la línea BC recorre la línea BA. Teniendo lugar tal movimiento, las líneas AB, BC, se cortarán entre sí en el punto F y describirá una línea cóncava BFH llamada Cuadratriz de Dinóstrato.
Dado un círculo; se requiere encontrar un cuadrado de la misma área.
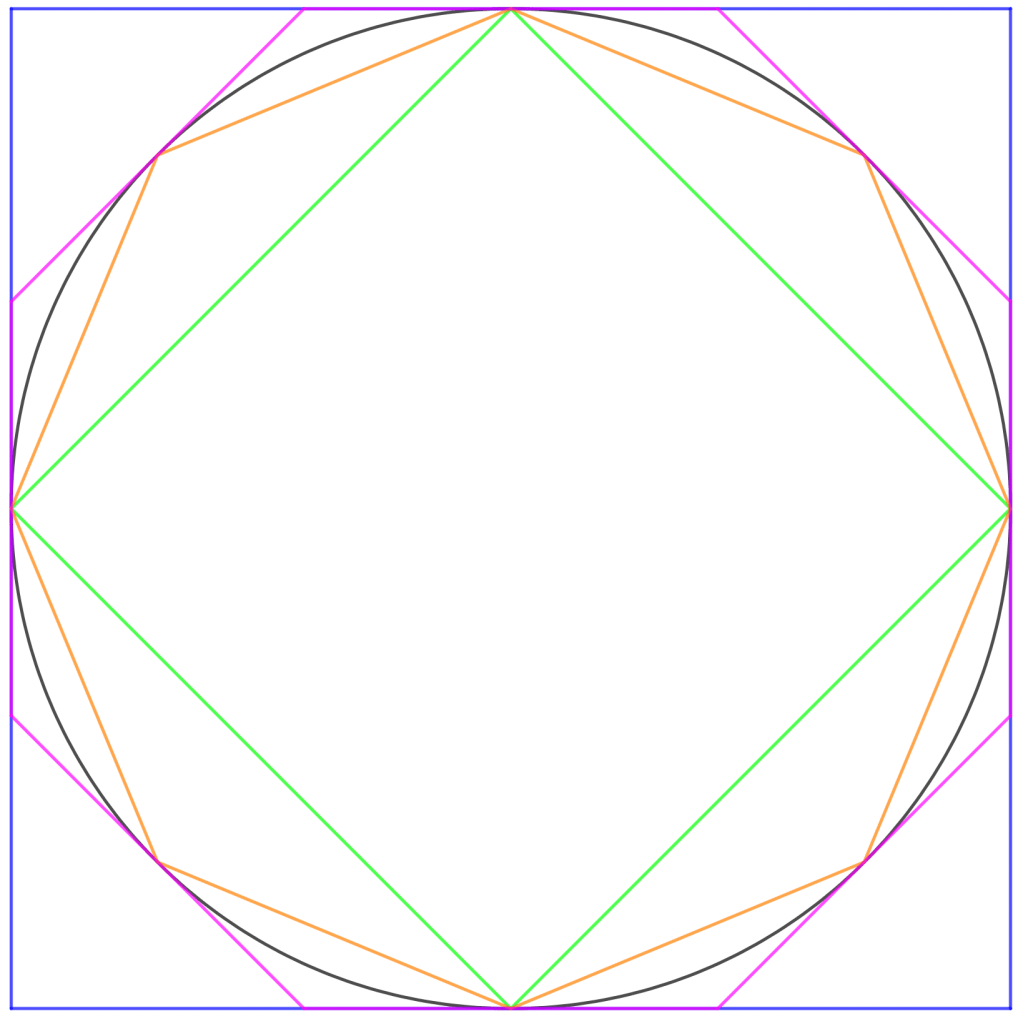
Euclides en los Elementos muestra que podemos inscribir y circunscribir polígonos regulares de 
lados de manera que la diferencia entre el área del círculo y los polígonos (inscritos y circunscritos) se puede hacer tan pequeña que cualquier área dada (ver Figura-2). Por otro lado, Euclides en los Elementos (libros I y II) describe un método para cuadrar cualquier figura rectilínea en el plano. Encuentra un cuadrado equivalente en área a la figura rectilínea dada. De esta forma, tenemos cuadrados de área menor o mayor a la del círculo, si consideramos un polígono inscrito o circunscrito, respectivamente. Entonces, por principio de continuidad para áreas, existe un cuadrado de área igual a la del círculo dado.
Ahora bien, todo se reduce a construir el segmento correspondiente al lado del cuadrado buscado. Arquímedes, en el tratado la medida del círculo, reduce el problema de la cuadratura del círculo al problema de encontrar un triángulo rectángulo cuya base es el perímetro del círculo y cuya altura es el radio del mismo. Así, pues, todo se reduce a rectificar la circunferencia, es decir, encontrar un segmento de línea recta equivalente en longitud a la circunferencia del círculo.
Los antiguos griegos encontraron varios procedimientos para rectificar la circunferencia, incluyendo al mismo Arquímedes con su Espiral, uno de ellos, la Cuadratriz de Dinóstrato, cuya propiedad principal por su descripción mecánica (Ver animación) es reducir la proporción de ángulos a la proporción de segmentos rectilíneos:
Haciendo AB=r, se puede ver que
Es decir, si r=1, 
rectifica un cuarto de circunferencia de un círculo de radio 1.
Las cónicas como aplicación de áreas
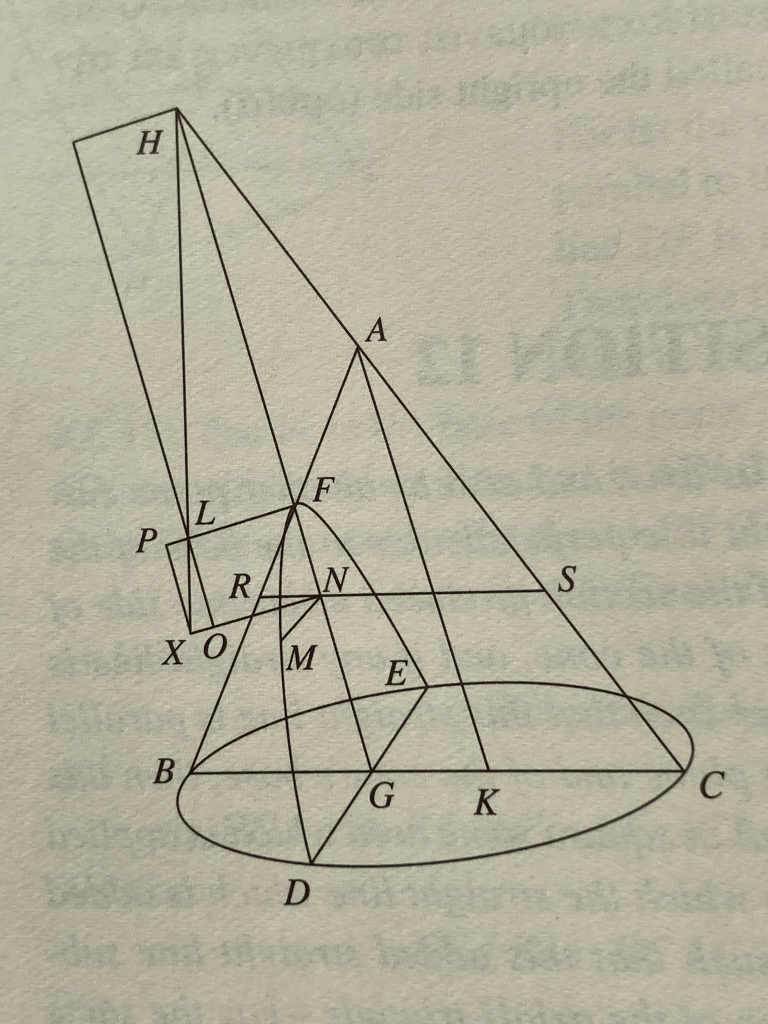
El cálculo del área en el plano, en la Antigüedad, se circunscribió al problema general de la cuadratura de cualquier figura. Sea ésta rectilínea o curvilínea. Es decir, encontrar un cuadrado equivalente en área a una figura dada. Consideremos el caso de cualquier figura rectilínea. Triangulando la figura y encontrando un paralelogramo por cada elemento de la triangulación cuyos lados sean paralelos a un ángulo dado y equivalente en área a dicho elemento (ver Animación: Triangulación figura rectilínea; Cálculo del área en la Antigüedad).
Basta con encontrar un método para sumar cualesquiera dos paralelogramos y, de esta forma, encontrar un paralelogramo equivalente en área a la figura dada. Ahora bien, dado que el ángulo dado (agudo y de color rojo) que determina el primer paralelogramo puede ser diferente al ángulo dado (recto y de color azul) que determina al segundo paralelogramo (ver Animación: Triangulación figura rectilínea). El método de aplicación de áreas encuentra su origen en desarrollar un método que nos permita sumar dos paralelogramos (color naranja y color azul, respectivamente) determinados por cualesquiera dos ángulos dados, encontrando, dos paralelogramos, equivalentes en área a los paralelogramos color naranja y azul, respectivamente, pero cuyos lados sean paralelos a un ángulo común (color rojo, ver Animación).
Por otro lado, teniendo dos paralelogramos, color naranja y color azul, cuyos lados son paralelos a un ángulo común, puede suceder que, no compartan, ahora, un lado común para poder pegar ambos paralelogramos a través de dicho lado.
Así, pues, se requiere, dado un segmento (color verde), un ángulo (color rojo) y un paralelogramo (color naranja), encontrar un paralelogramo cuyos lados sean paralelos a los lados del ángulo dado, cuya base sea el lado dado y equivalente en área al paralelogramo dado (ver Figura: Aplicación de área por yuxtaposición).
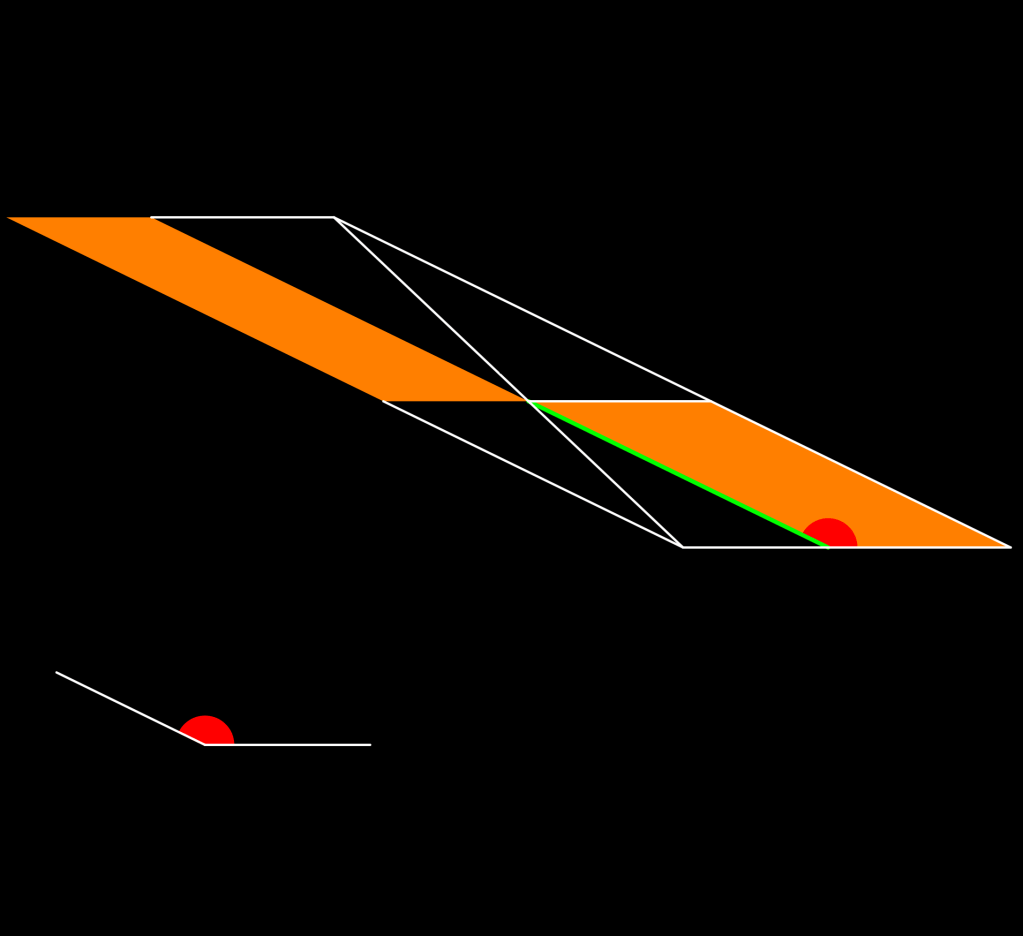
Cuando el ángulo dado es un ángulo recto, el paralelogramo dado se convierte en un rectángulo.
En suma, cuadrar cualquier figura rectilínea es equivalente a cuadrar cualquier rectángulo. De esta forma, si consideramos un rectángulo dado de base PB y altura PD. Y, con diámetro AB (AP=PD), trazamos una circunferencia, y ortogonal en P, consideramos el segmento PE. Entonces, por potencia interior de un punto P respecto a una circunferencia, se cumple que el cuadrado construido sobre PE es igual en área al rectángulo dado (color amarillo, ver Figura: Cuadratura de un rectángulo).
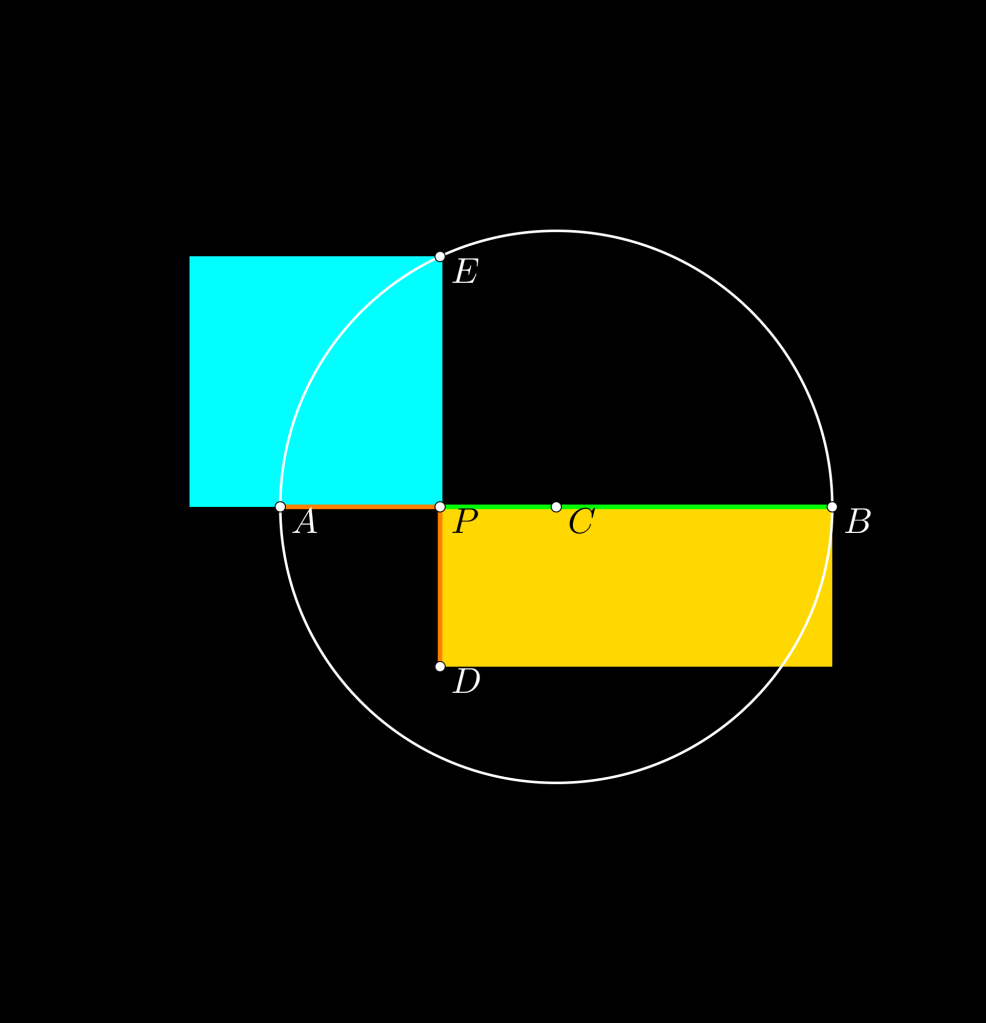
Ahora bien, si nos es dado un segmento (color rojo) y un área rectilínea (que podemos suponer sin perdida de generalidad que es un cuadrado cuyo lado es color fiusha), el método de aplicación del área dada –cuando ésta varia de forma continua– sobre el segmento dado –y fijo– por yuxtaposición, genera una rama de una parábola (ver Animación).
Por otro lado, si nos es dado un segmento (color rojo) y un área rectilínea (que podemos suponer sin perdida de generalidad que es un cuadrado cuyo lado es color fiusha), el método de aplicación del área dada –cuando ésta varia de forma continua– sobre el segmento dado –y fijo– y que excede en un cuadrado de lado x (color amarillo), genera una rama de una hipérbola (ver Animación).
Pero, si nos es dado un segmento (color rojo) y un área rectilínea (que podemos suponer sin perdida de generalidad que es un cuadrado cuyo lado es color fiusha), el método de aplicación del área dada –cuando ésta varia de forma continua– sobre el segmento dado –y fijo– y que es deficiente en un cuadrado de lado x (color amarillo), genera un arco de circunferencia (ver Animación).
O, si nos es dado un segmento (color rojo) y un paralelogramo equivalente a una área dada, el método de aplicación del área dada –cuando ésta varia de forma continua– sobre el segmento dado –y fijo– y que es deficiente en un paralelogramo semejante al paralelogramo dado, genera un arco de elipse (ver Animación).
israelramos.mx 