¿Qué es el cálculo?
En la Antigüedad, Euclides y Arquímedes, hicieron uso de un principio de divisibilidad infinita que subyace a todas las cantidades de la geometría: figuras, sólidos y ángulos, para calcular el área de un círculo, el volumen de una pirámide y el área de la espiral (de Arquímedes), respectivamente. Y el principio de divisibilidad infinita para segmentos para mostrar la inconmensurabilidad de la diagonal de un cuadrado respecto a su lado. Este principio hoy día lo conocemos como el principio Arquimediano. En este sentido, el principio que subyace a la naturaleza de las diferentes cantidades de la geometría es el principio de continuidad:
El principio Arquimediano introduce el principio de continuidad en geometría.
David Hilbert
Mismo que subyace al origen del cálculo diferencial e integral. Razón por la cual para comprender qué es el cálculo es menester volver a sus orígenes.
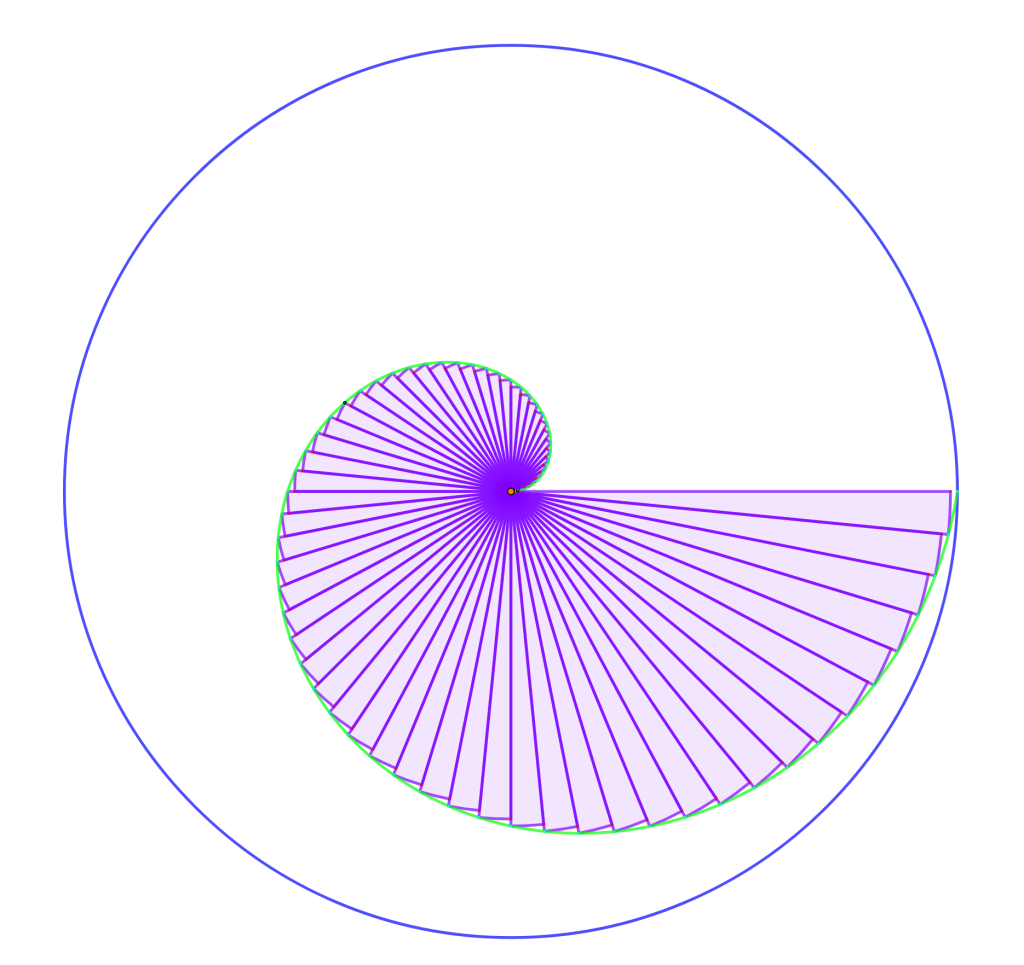

Principio de divisibilidad infinita para segmentos para mostrar la inconmensurabilidad de la diagonal de un cuadrado respecto a su lado.
