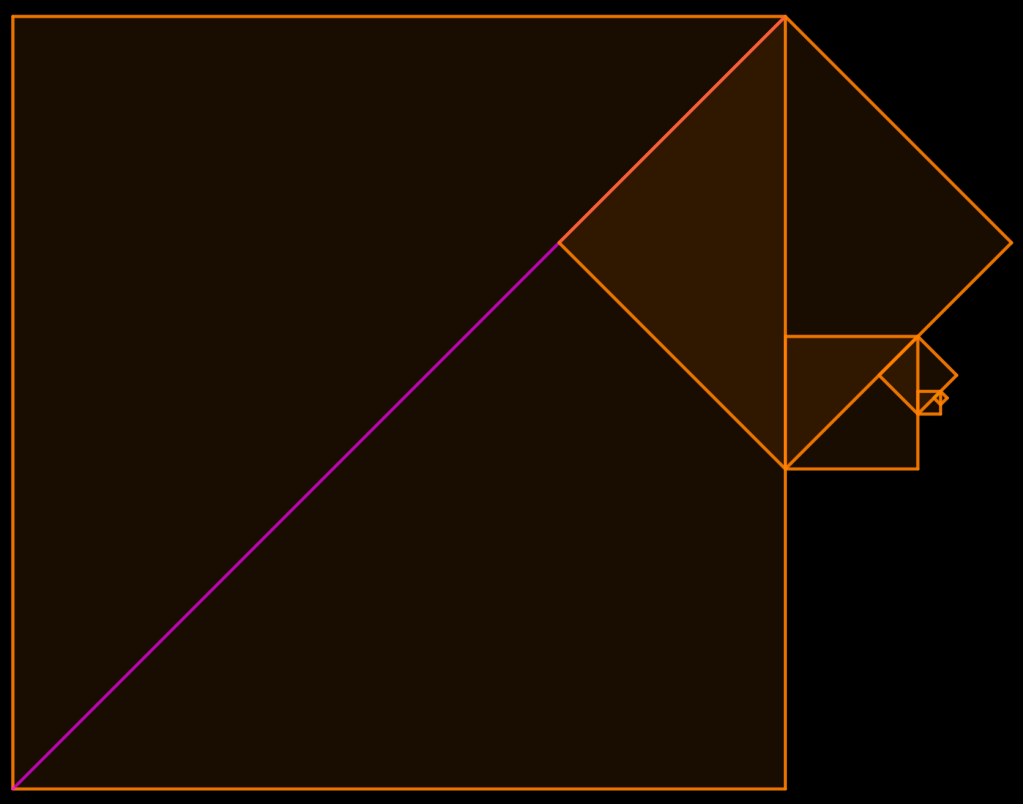
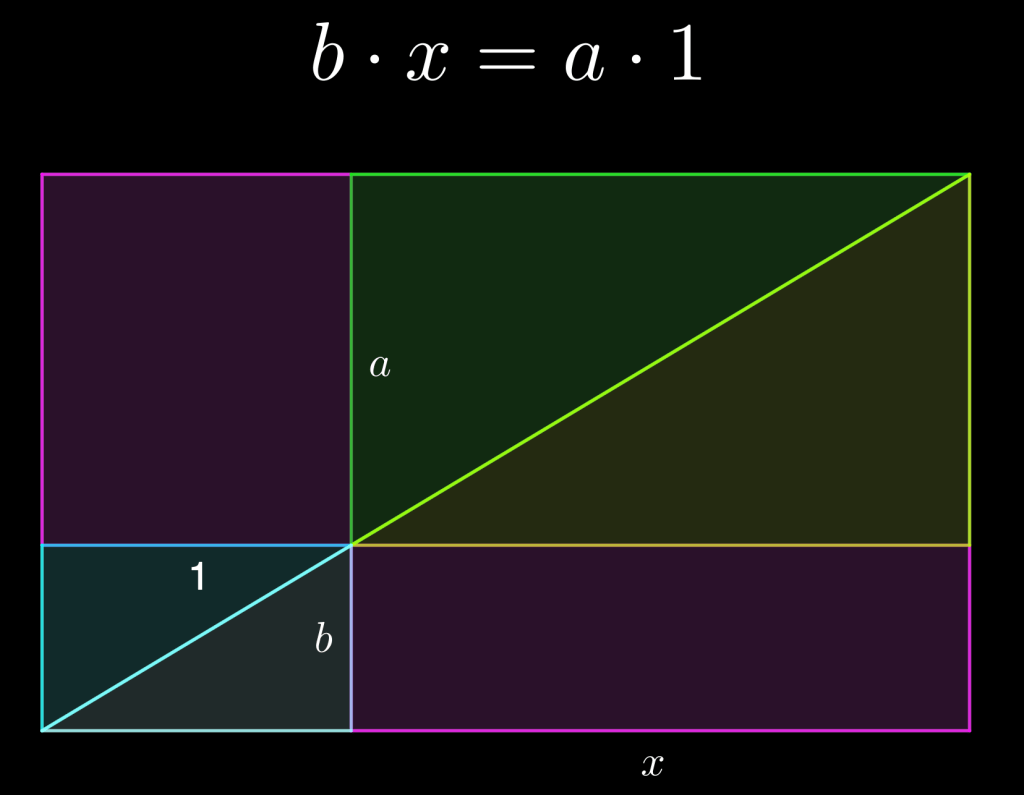Algoritmo de la División

---

Resolver, en general, la ecuación: nx=m, con n y m números naturales, o, bx=a, con a y b segmentos de línea recta. Nos conduce, en la primera ecuación, a observar que cuando n divide a m, ésta, tiene solución en los números naturales. En caso contrario, cuando n no divide a m, por el algoritmo de la división, m=kn+r, con k y r números naturales; 0<r<k. Es decir, esta ecuación no tiene solución en los números naturales.

Para la segunda ecuación, contrario al primer caso, ésta siempre tiene solución, es decir, siempre existe un segmento de línea recta tal que x=a/b.

Contrario a lo que se suele pensar de la matemática griega, Euclides, en la Antigüedad, desarrollo un método, llamado método de aplicación de áreas, que le permitió sumar áreas (de cualesquiera dos figuras rectilíneas en el plano) y, en particular, le permitió dividir cualesquiera dos segmentos línea recta. ¡Los griegos sabían dividir!

Ahora bien, la aritmética hace uso de aproximaciones para calcular la raíz cuadrada de un número (no cuadrado perfecto). Por otro lado, en la geometría el cálculo de la raíz cuadrada de cualquier segmento es exacto. El proceso de división en la aritmética:

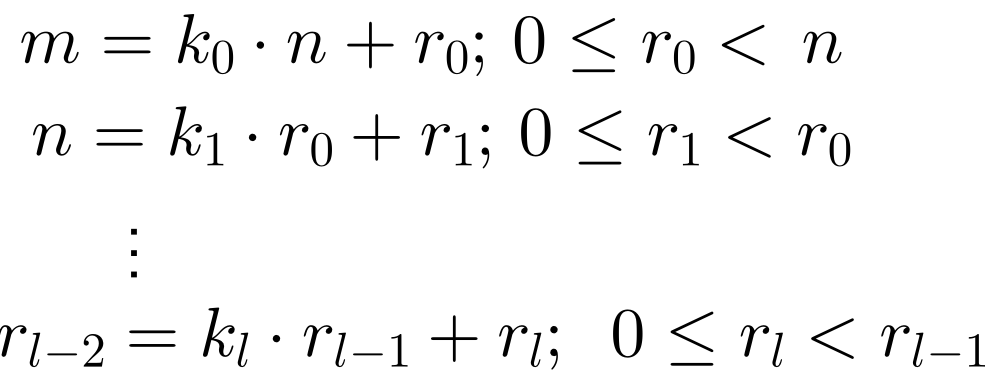
termina para cualesquiera dos números naturales n y m. En la geometría, el proceso de división análogo, para segmentos de línea recta b y a (b entre a) cuya proporción: k=a/b, 0<k<1, no termina.

Esta diferenciación que subyace a la aritmética y a la geometría, a saber, la que subyace al principio de divisibilidad finita que caracteriza la naturaleza de las magnitudes discretas (números) y la que subyace al principio de divisibilidad infinita que caracteriza la naturaleza de las magnitudes continuas (segmentos de línea recta), nos invita a continuar con el análisis comparativo entre ambas magnitudes. Todo a la luz de comprender lo común entre ambas que, a su vez, nos permite el ascenso a la generalidad. Es decir, buscamos abstraer en la medida en que aspiramos a la generalidad.

Abstraer significa olvidar

J. L. Borges

… toda investigación consiste en la investigación comparativa, sea ésta fácil o difícil… Por su parte la proporción, dado que implica la conveniencia en algo uno y simultáneamente también la alteridad, no puede ser entendida sin el número. Por lo tanto, el número incluye todas las cosas proporcionales. De aquí que el número no es el que realiza la proporción únicamente respecto de la cantidad, sino en todas las cosas que de alguna manera, sea sustancial sea accidentalmente, pueden convenir y diferir. Quizá por esto Pitágoras consideraba que todas las cosas son constituidas y entendidas por la fuerza propia de los números.

Nicolás de Cusa