
«Las relaciones más sencillas son las más comunes, y éste es el fundamento en el que descansa la inducción».
— Pierre-Simon Laplace
Algoritmo de Euclides: Máximo Común Divisor

Partiendo del hecho:
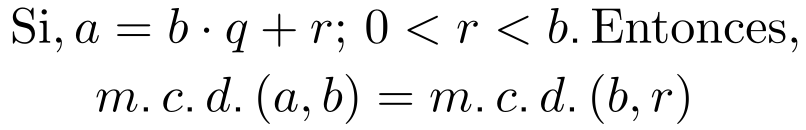
y aplicando el algoritmo de la división, obtenemos:
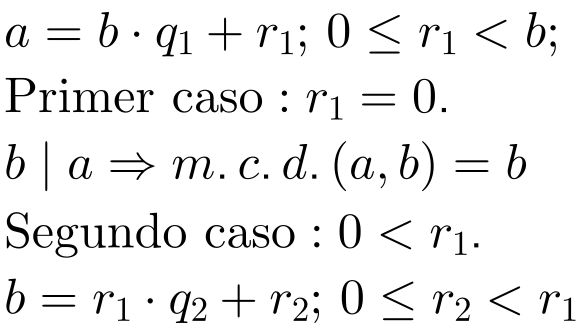
Volviendo a iterar el algoritmo de la división:
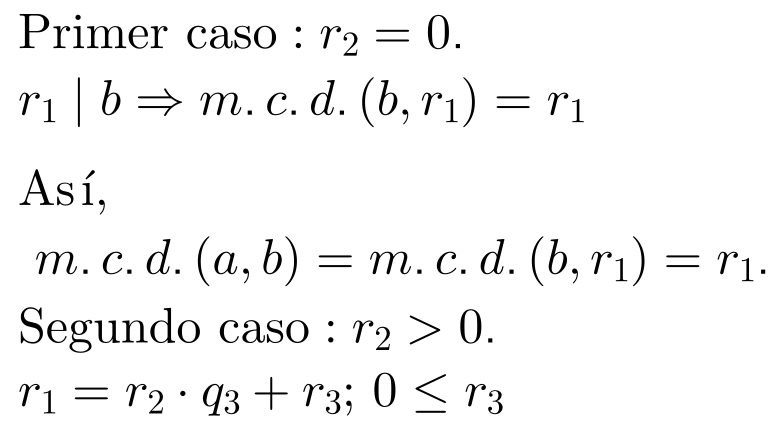
En general:
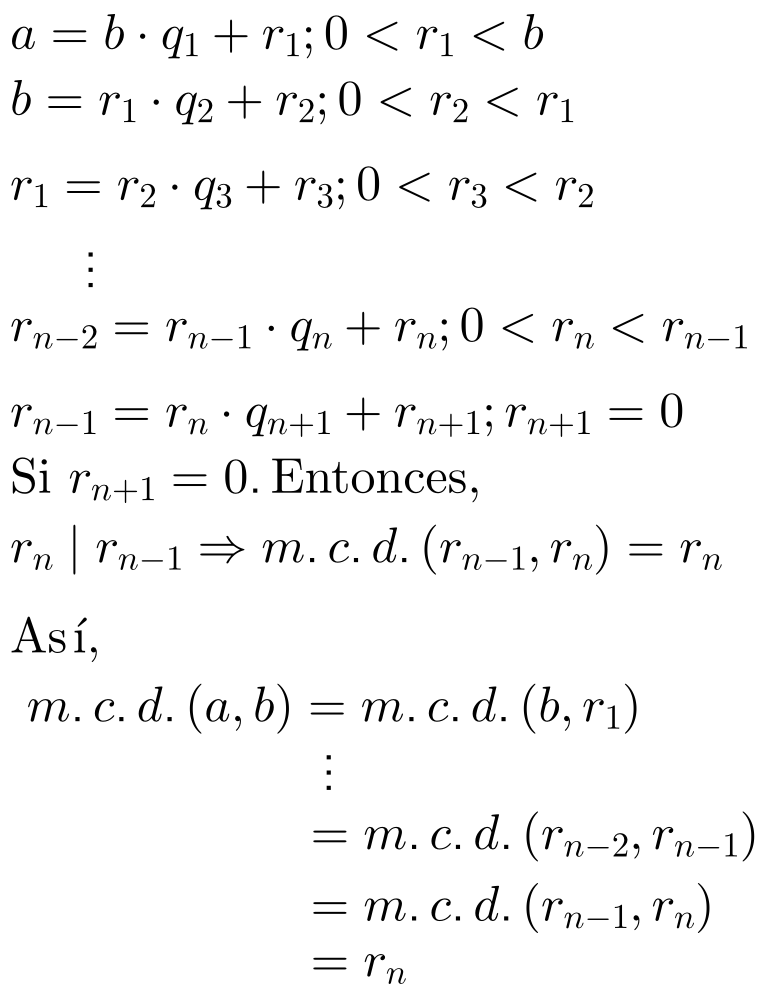
Ahora bien, el proceso en general, necesariamente, tiene que terminar por Principio del Buen Orden o por el hecho de que no podemos tener una cadena infinita descendente de números naturales:
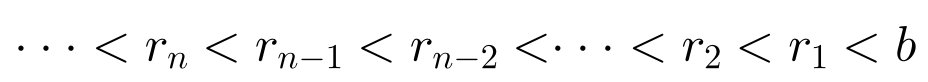
Por otro lado, el procedimiento anterior nos permite expresar al Máximo Común Divisor como combinación lineal entera de a y b. Despejando r1 de la primera igualdad, expresamos a r1 en términos de a y b: r1(a, b); Sustituyendo en la segunda igualdad y despejando r2, expresamos a r2 en términos de a y b: r2(a, b); Análogamente para r3, expresamos a r3 en términos de a y b: r3(a, b). En general, podemos expresar a rn en términos de a y b: rn(a, b), es decir, podemos expresar al máximo común divisor, rn, de a y b como combinación lineal entera de a y b.
Partiendo del siguiente hecho:
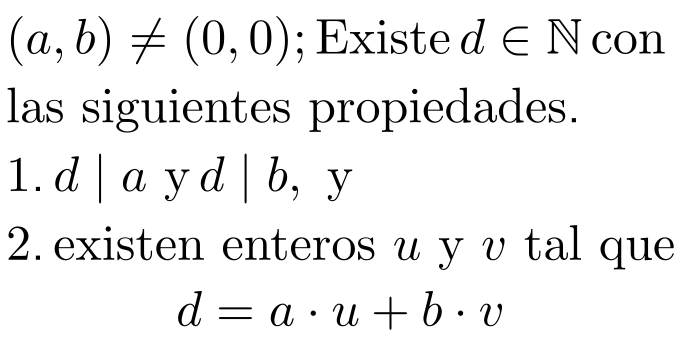
Buscamos encontrar las soluciones enteras de la ecuación lineal.

Primer caso: (El máximo común divisor g, de m y n, divide a d).
Si m. c. d (m, n)=g, entonces m. c. d. (m/g, n/g)=1; Haciendo k1=m/g, k2=n/g, k3=d/g y, por lo observado anteriormente, para d=1, existen enteros x0, y0 tal que

Multiplicando la igualdad anterior por d.
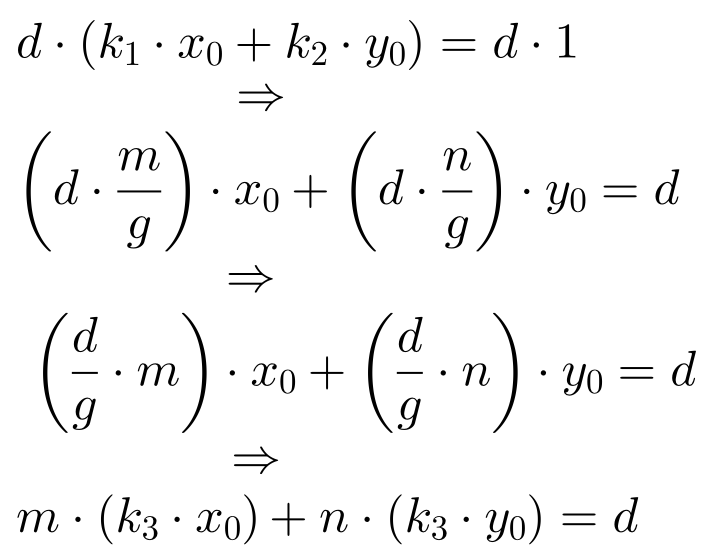
Haciendo x‘0=k3x0 y y‘0=k3y0, la solución general es:
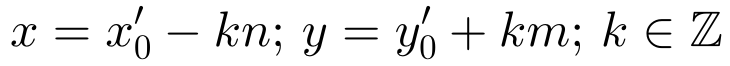
Segundo caso: (El máximo común divisor g, de m y n, no divide a d).
Afirmamos que la ecuación lineal no tiene soluciones enteras. En efecto, supongamos por, reductio ad absurdum, que existen enteros, x0 y y0, tal que
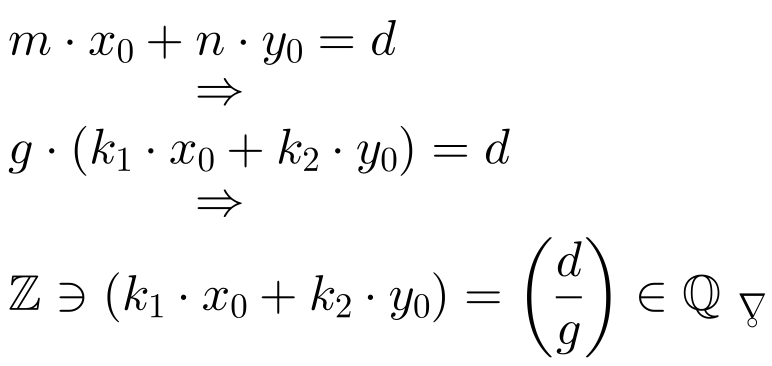
Ahora bien, encontrar las soluciones enteras de la ecuación lineal, es, encontrar los puntos de coordenadas enteras que pertenecen a la línea recta cuya ecuación es (ver Figura):

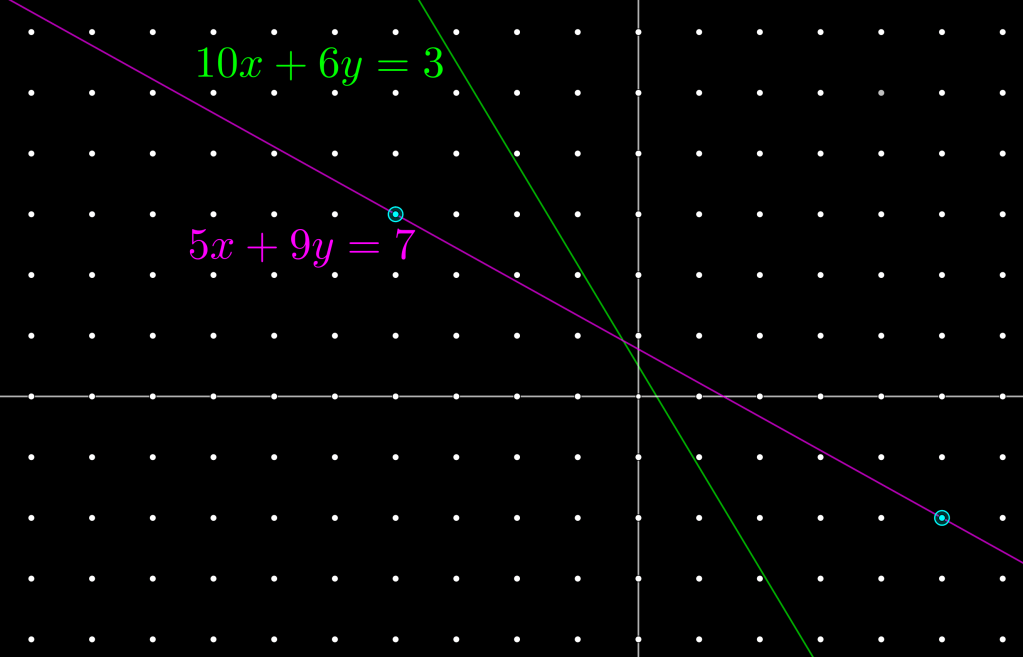
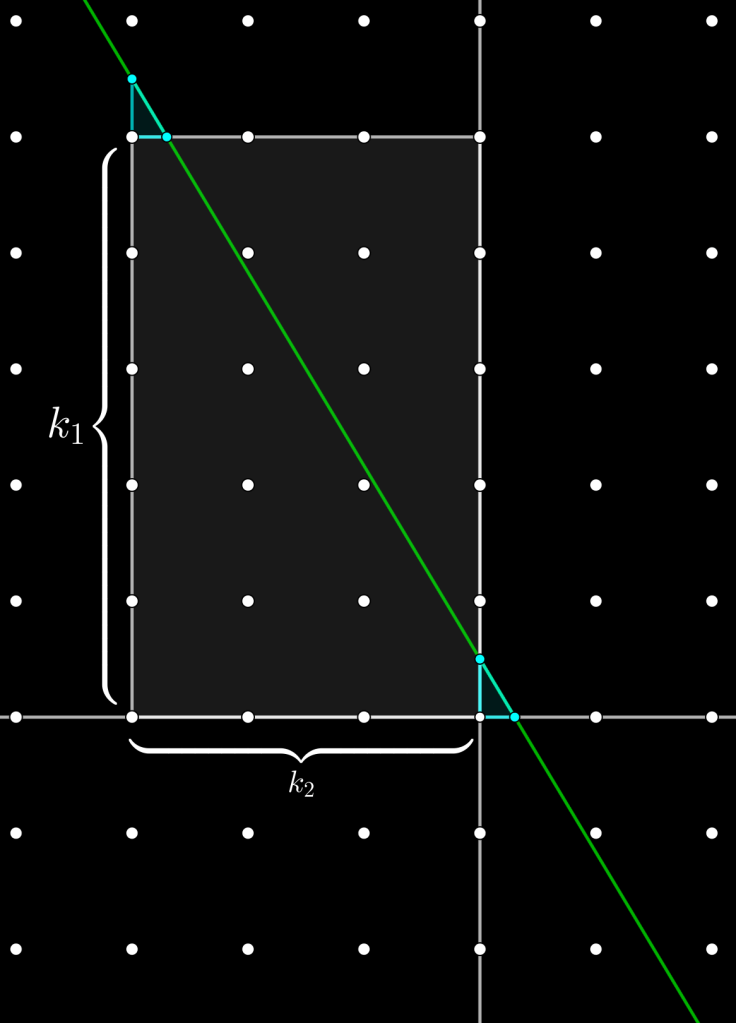
Notemos que si una línea recta: mx+ny=d, en un rectángulo como el que se muestra en la Figura, de base k2 y altura k1, no contiene puntos de coordenadas enteras pertenecientes a este rectángulo, entonces no contiene ningún punto del plano de coordenadas enteras. Lo cual sucede si m. c. d. g, de m y n, no divide a d. Donde k1=m/g y k2=n/g.
En efecto, primero, notemos que no puede existir un punto de coordenadas enteras contenido en el rectángulo que satisfaga la ecuación lineal. En caso contrario, si existen enteros x0 y y0 tal que (x0, y0) pertenece al rectángulo y mx0+ny0=d. Así,
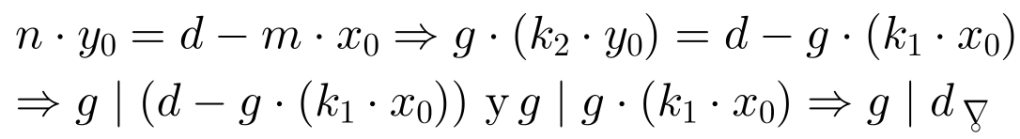
Por otro lado, si la recta no contiene puntos de coordenadas enteras que pertenezcan al rectángulo, entonces no contiene ningún punto del plano de coordenadas enteras. Ya que el comportamiento de la línea recta se repite después de cruzar los lados del rectángulo, como se muestra en la Figura con los triángulos color azul celeste. Mostremos que ambos triángulos son congruentes, es decir, basta mostrar que tienen la misma altura, ya que al tener ángulos correspondientes de las bases iguales, tendrían bases iguales y, por el criterio, Lado-Ángulo-Lado o Ángulo-Lado-Águlo, los dos triángulos serían congruentes. En efecto, para uno de los triángulos se tiene, haciendo x=0, que la altura es y=d/n. Para el otro, haciendo x=-k2, la altura es y-k1=(d/n+(m/n)k2)-k1=(d/n+(k1/k2)k2)-k1=(d/n+k1)-k1=d/n.
Ahora bien, si g | d, entonces, como se ha mostrado anteriormente, encontrar las soluciones enteras de la ecuación lineal: mx+ny=d, se reduce a encontrar las soluciones enteras de la ecuación: k1x+k2y=1, donde m=gk1; n=gk2; d=gk3; m. c. d. (m, n)=g (así, m. c. d. (k1=m/g, k2=n/g)=1). Y, como se muestra en la figura, no obstante que las dos rectas asociadas a las dos ecuaciones: k1x+k2y=1 y mx+ny=d, teniendo la misma pendiente y siendo una, mx+ny=d, la traslación de la otra, k1x+k2y=1. Las soluciones enteras de una no son las soluciones enteras de la traslación de la otra (ver Figura).

