Cálculo del área en la Antigüedad
Equidescomposición
En la Antigüedad, la falta de una unidad en la geometría condujo a los geómetras a medir a través de comparar cantidades de la misma naturaleza (cantidades homogéneas). De esta forma, la equidescomposición: descomponer una figura en figuras menores y reordenarlas para formar otra figura de la misma área; y la equicomplementariedad: agregar figuras (de la misma área) a una figura dada para formar dos figuras de la misma área, fueron dos procedimientos que permitieron mostrar que, si a iguales les quitamos cosas iguales, lo que nos queda son cosas iguales. Si a iguales les agregamos cosas iguales, lo que resulta son cosas iguales. Así, pues, estos dos métodos permitieron a Euclides mostrar:
Paralelogramos de la misma base y entre las mismas paralelas son iguales entre sí (paralelogramos que tienen la misma base y alturas iguales, tienen la misma área).
Lo anterior sin determinar una fórmula para el cálculo del área de un paralelogramo, ya que no había una unidad de medida.
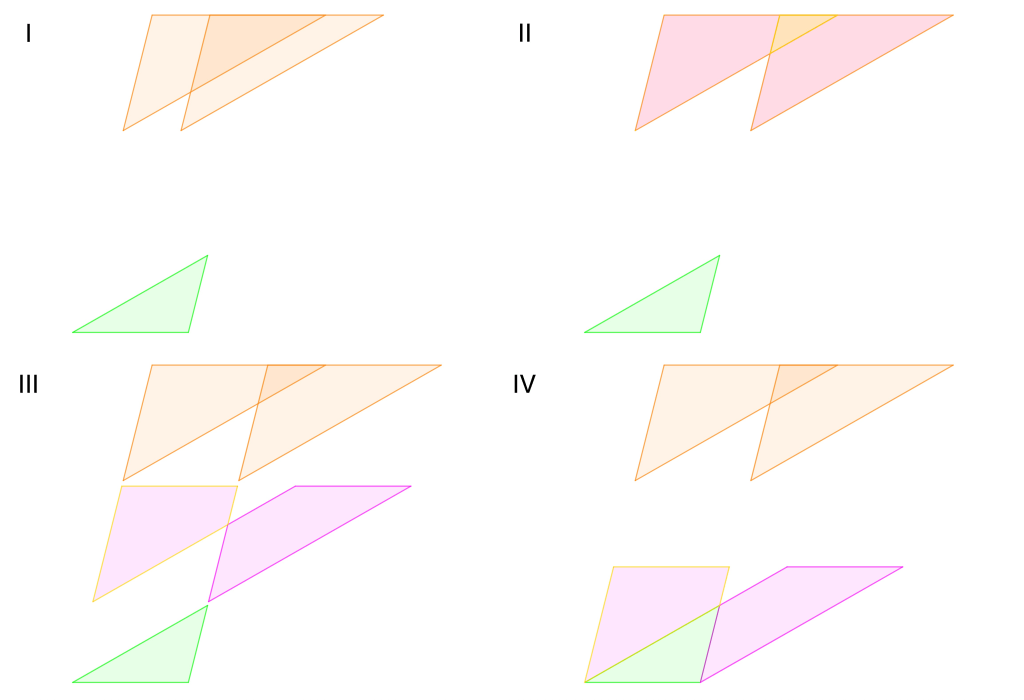
De izquierda a derecha y de arriba a abajo (ver la figura):
I: Traslación de un triángulo (pintado de naranja) no cambia su área.
II: Si a áreas iguales (triángulos naranjas) substraemos una misma área (triángulo amarillo), lo que nos queda (trapecios rosas) tienen la misma área.
III: Traslación de áreas (trapecios rosas), iguales, no cambia su área.
IV: Si a un área (triángulo verde) le agregamos cosas iguales (trapecios rosas), lo que obtenemos tendrá la misma área (los paralelogramos tendrán la misma área).
Principio de divisibilidad infinita
¿Qué es el cálculo?
En la Antigüedad, Euclides y Arquímedes, hicieron uso de un principio de divisibilidad infinita que subyace a todas las cantidades de la geometría: figuras, sólidos y ángulos, para calcular el área de un círculo, el volumen de una pirámide y el área de la espiral (de Arquímedes), respectivamente. Este principio hoy día lo conocemos como el principio Arquimediano. En este sentido, el principio que subyace a la naturaleza de las diferentes cantidades de la geometría es el principio de continuidad:
El principio Arquimediano introduce el principio de continuidad en geometría.
David Hilbert
Mismo que subyace al origen del cálculo diferencial e integral. Razón por la cual para comprender qué es el cálculo es menester volver a sus orígenes.
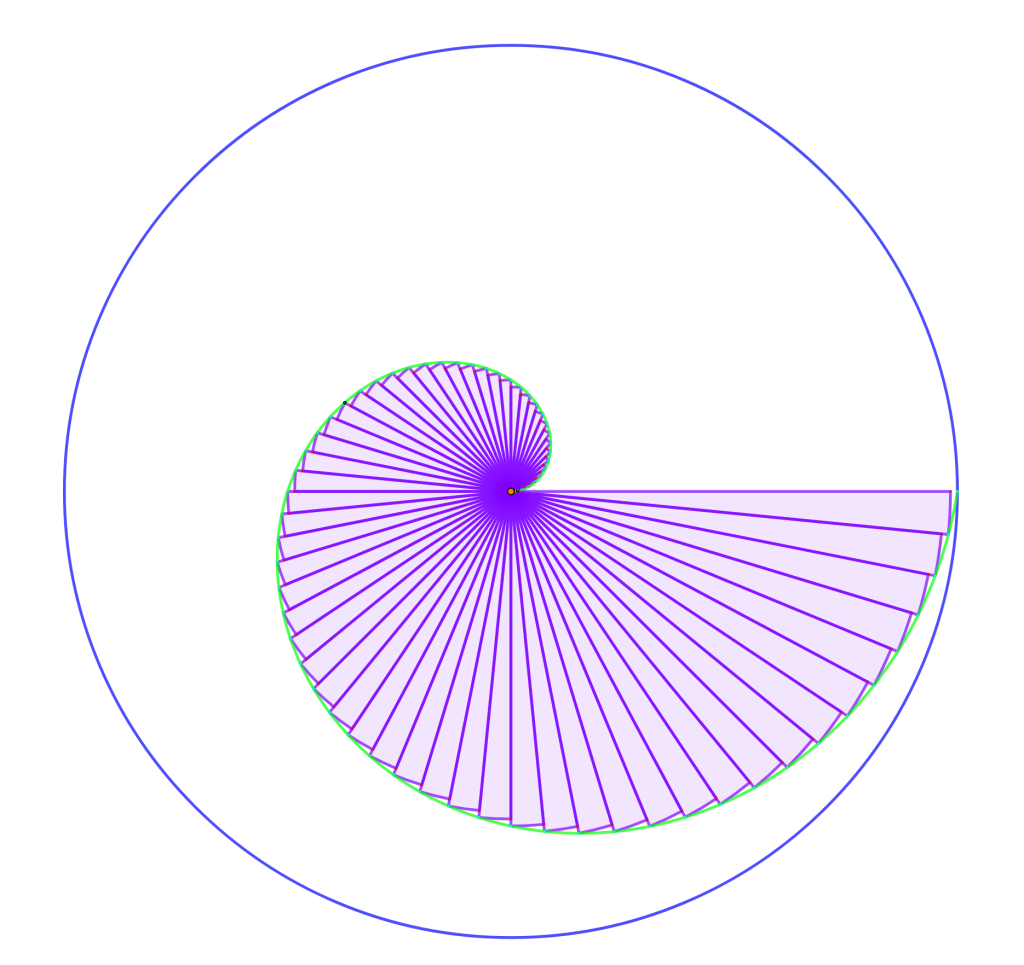

Principio de divisibilidad infinita para segmentos para mostrar la inconmensurabilidad de la diagonal de un cuadrado respecto a su lado.
Lo insoslayable del infinito en la comprensión de lo finito
Principio de divisibilidad infinita o sobre el concepto de límite
El concepto de límite, concepto fundamental que subyace al cálculo diferencial e integral, toda vez que, la continuidad, la derivada y la integral, se definen a través de éste. Encuentra su motivación en la Antigüedad con el «cálculo del área del círculo» y el «cálculo del área de la espiral», debido a Euclides y Arquímedes, respectivamente. La necesidad de acompañar el concepto formal -de límite- con la idea intuitiva del principio de divisibilidad infinita para áreas y del principio de divisibilidad infinita para ángulos que, a su vez, subyacen al cálculo de los dos ejemplos antes mencionados, respectivamente. Objetivo, éste, de nuestro interés para motivar un primer curso de Cálculo Diferencial e Integral.

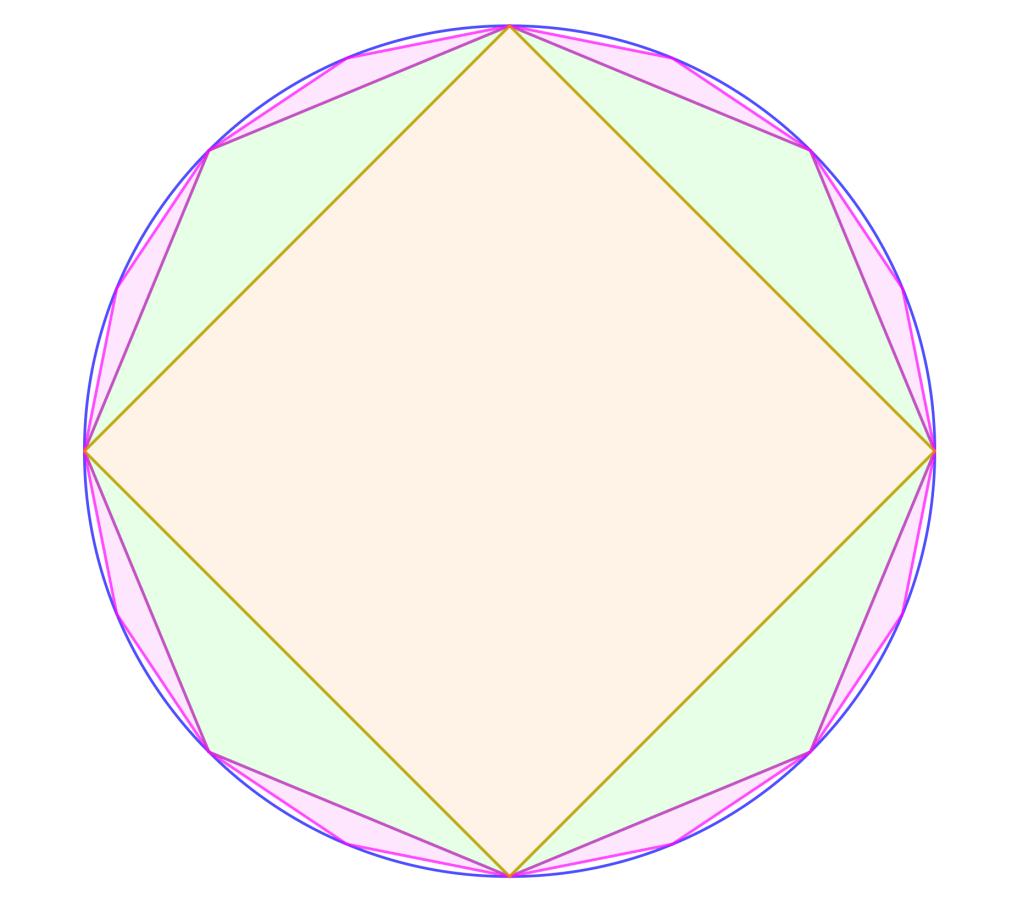
Principio de Divisibilidad Infinita para áreas para calcular el área de un círculo.
